Prebrojavanje savršenih sparivanja
Sadržaj
1Uvod
Mnogi se životni problemi mogu modelirati uz pomoć grafova. Graf se sastoji od točaka i njihovih spojnica. Tako točke mogu biti ljudi u određenom društvu, a spojnice parovi prijatelja, ili točke mogu biti električne komponente, a spojnice električna mreža itd.
Grubo govoreći, graf je familija točaka, koje nazivamo vrhovima, zajedno sa spojnicama među njima, koje nazivamo bridovima. Precizna definicija glasi:
Definicija 1. Graf je uređena trojka G=(V,E,\varphi), gdje je V neprazan skup vrhova, E skup bridova koji je disjunktan s V, a \varphi funkcija koja svakom bridu iz E pridružuje dva, ne nužno različita vrha iz V. Graf često zapisujemo kao par G=\left( V,E\right) ili samo G.
Ako su nekom bridu e\in E pridruženi vrhovi u,v\in V, kažemo da su u i v krajevi brida e. Kažemo još i da su vrhovi u i v incidentni s bridom e, da su u i v susjedni vrhovi te pišemo e=uv. Bridovi s barem jednim zajedničkim krajem zovu se susjedni bridovi. Brid čiji se krajevi podudaraju zove se petlja, a brid čiji su krajevi različiti pravi brid ili karika. Dva ili više bridova koji imaju isti par krajeva zovu se višestruki bridovi. Graf koji nema petlji i višestrukih bridova nazivamojednostavnim grafom. Mi ćemo se ovdje baviti samo jednostavnim grafovima i pod pojmom graf podrazumijevati samo takve grafove.

Definicija 2. Šetnja W u grafu G konačan je niz v_{0}e_{1}v_{1} e_{2}v_{2}...v_{m-1}e_{m}v_{m} čiji su članovi naizmjence vrhovi i bridovi grafa G sa svojstvom da su krajevi brida e_{i} vrhovi v_{i-1} i v_{i}, za svaki i=1,...,m. Za vrh v_{0} kažemo da je početak, a za vrh v_{m} kraj šetnje W.
Primijetimo da je u jednostavnom grafu šetnja potpuno određena nizom svojih vrhova v_{0}v_{1}v_{2}...v_{m-1}v_{m}.
Definicija 3. Šetnja u kojoj su svi bridovi različiti naziva se staza. Ako su pritom i svi vrhovi, osim eventualno početnog i krajnjeg, različiti, takvu stazu nazivamo put. Za šetnju kažemo da je zatvorena ako je v_{0}=v_{m}, a zatvoreni put nazivamo ciklusom.
Da bismo dobili predodžbu o tome kakvim se problemima bavi teorija sparivanja, počnimo s dva jednostavna primjera koja dobro ilustriraju taj problem.
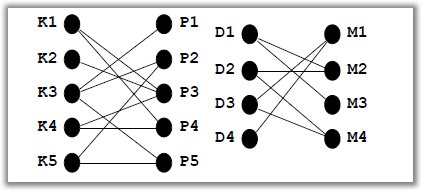
Primjer 4. U nekom društvu, koje se sastoji od četiri djevojke D_{1},D_{2},D_{3},D_{4} i četiri momka M_{1},M_{2},M_{3},M_{4}, postoje neke uzajamne simpatije. Naime, djevojka D_{1} simpatizira momke M_{2} i M_{3}, djevojka D_{2} momke M_{2} i M_{4}, djevojka D_{3} momke M_{1} i M_{4}, te djevojka D_{4} simpatizira momka M_{1}. Odredite koliko najviše parova možemo povezati poštujući navedene simpatije?
Primjer 5. Neko poduzeće dalo je oglas za zapošljavanje novih djelatnika na poslove P_{1},P_{2},P_{3},P_{4} i P_{5}. Na oglas se prijavilo pet kandidata K_{1},K_{2},K_{3},K_{4} i K_{5}, s tim da je kandidat K_{1} kvalificiran za poslove P_{3} i P_{4}, kandidat K_{2} za posao P_{3}, kandidat K_{3} za poslove P_{1},P_{2} i P_{3}, kandidat K_{4} za poslove P_{3} i P_{4} te kandidat K_{5} za poslove P_{2} i P_{5}. Ispitajte je li moguće rasporediti kandidate na poslove tako da se svi poslovi obavljaju i da svaki kandidat obavlja posao za koji je kvalificiran?
Ako izvršitelje i poslove, odnosno djevojke i momke, uzmemo za vrhove grafa, a bridovima spojimo svakog izvršitelja s poslovima koje zna obavljati, odnosno sve djevojke i momke koji se međusobno simpatiziraju, onda naš problem glasi: odredite maksimalan broj bridova od kojih nikoja dva nisu susjedna.
2Sparivanje u grafovima
Definicija 6. Sparivanje u grafu G=(V,E) je skup bridova M\subseteq E koji su karike i koji nisu međusobno susjedni. Kažemo da su vrhovi u i v spareni u M ako su u i v krajevi nekog brida iz M.
Ako je E\neq\emptyset, onda je svaki jednočlani podskup od E jedan primjer sparivanja u G. No, zanimljivo je naći sparivanje sa što većim brojem bridova. Stoga definiramo:
Definicija 7. Sparivanje M u grafu G je maksimalno sparivanje u G ako ne postoji sparivanje u G s većim brojem bridova od broja bridova u M.
Definicija 8. Kažemo da sparivanje M u grafu G=(V,E) zasićuje vrh v\in V ili da je vrh v M-zasićen ako je v kraj nekog brida iz M. U protivnom kažemo da je vrh v M-nezasićen. Kažemo da je sparivanje M savršeno sparivanje ako je svaki vrh iz G M-zasićen.
U literaturi se savršeno sparivanje često zove Kekuléova struktura, prema njemačkom kemičaru Augustu Kekuléu (1829. – 1896.).
Očito je svako savršeno sparivanje ujedno i maksimalno, dok obrat općenito ne vrijedi. Nadalje, broj bridova u savršenom sparivanju je konstantan i iznosi \frac{\left\vert V\right\vert }{2}. Za postojanje savršenog sparivanja nužno je da graf ima paran broj vrhova. No, to je samo nuždan, a ne i dovoljan uvjet za postojanje savršenog sparivanja. Osnovni problem teorije sparivanja jest ispitati postoji li savršeno sparivanje i ako postoji, konstruirati ga. U slučaju da se ne može konstruirati savršeno sparivanje, cilj je konstruirati sva ili bar neka maksimalna sparivanja.
Definicija 9. Za skup vrhova S\subseteq V grafa G=\left( V,E\right) kažemo da je stabilan ako nikoja dva vrha iz S nisu susjedna. Vršni pokrivač K\subseteq V je skup vrhova grafa G takvih da svaki brid od G ima barem jedan kraj u K. Bridni pokrivač L\subseteq E je skup bridova grafa G takvih da je svaki vrh grafa G kraj barem jednom bridu iz L.
Označimo s
| \bullet | v(G)= kardinalnost maksimalnog sparivanja u G, |
| \bullet | \alpha(G)= kardinalnost maksimalnog stabilnog skupa u G, |
| \bullet | \tau(G)= kardinalnost minimalnog vršnog pokrivača od G, |
| \bullet | \rho(G)= kardinalnost minimalnog bridnog pokrivača od G. |
Primijetimo da je \rho(G) dobro definiran samo za grafove bez izoliranih vrhova.
Neka je K neki vršni pokrivač grafa G, a M neko sparivanje u G. Tada svaki brid iz M ima barem jedan kraj u K, a budući da bridovi iz M nemaju zajedničkih vrhova, to je \left\vert M\right\vert \leq\left\vert K\right\vert. Stoga i za maksimalno sparivanje M^{\ast} i minimalni vršni pokrivač \bar{K} također vrijedi \left\vert M^{\ast}\right\vert \leq\left\vert \bar{K}\right\vert, tj. \upsilon (G)\leq\tau(G).
Slično, ako je L bridni pokrivač grafa G, a S stabilan skup, onda je \left\vert S\right\vert \leq\left\vert L\right\vert jer je svaki vrh iz S kraj barem jednom bridu iz L, a nikoja dva vrha iz S nisu susjedna. Stoga je \alpha(G)\leq\rho(G). Nadalje, vrijedi teorem
Teorem 10. Skup S je stabilan ako i samo ako je skup V\setminus S vršni pokrivač grafa G=(V,E).
Iz ovog odmah slijedi da je \alpha(G)+\tau\left( G\right) =\left\vert V\right\vert . Slično, v(G)+\rho\left( G\right) =\left\vert V\right\vert, tj. kardinalnost maksimalnog sparivanja i minimalnog bridnog pokrivača u sumi daju ukupan broj bridova grafa G, iako komplement sparivanja ne mora biti bridni pokrivač, kao što je slučaj sa stabilnim skupom i vršim pokrivačem.
Jedan od osnovnih pojmova teorije sparivanja je pojam uvećavajućeg puta.
Definicija 11. Neka je M sparivanje u grafu G=\left( V,E\right). M-alternirajući put u G je put čiji su bridovi naizmjenice elementi iz skupova M i E\setminus M.
M-uvećavajući put u G je M-alternirajući put čiji su početak i kraj M-nezasićeni vrhovi.
M-uvećavajući put u G je M-alternirajući put čiji su početak i kraj M-nezasićeni vrhovi.

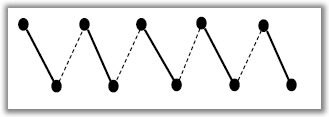
Teorem 12. [C. Berge, 1957.] Sparivanje M u grafu G je maksimalno sparivanje ako i samo ako G ne sadržava M-uvećavajući put.
Ovaj teorem omogućuje nam da provjerimo je li neko sparivanje M u grafu G maksimalno, kako bismo ispitali postoji li ili ne M-uvećavajući put.
2.1Sparivanje u bipartitnom grafu
Definicija 13. Za graf G kažemo da je bipartitan ilidvodijelan ako se skup njegovih vrhova može podijeliti u dva disjunktna podskupa X i Y tako da svaki brid grafa G ima jedan kraj u X, a drugi u Y. Particija (X,Y) naziva se biparticija grafa G. Bipartitni graf s biparticijom (X,Y) označava se G(X,Y).
Vidjeli smo da u svakom grafu vrijedi nejednakost \upsilon(G)\leq\tau(G). No, sljedeći teorem kaže da u bipartitnom grafu vrijedi \upsilon (G)=\tau(G).
Teorem 14.[Kőnig–Egerváry, 1931.] U bipartitnom grafu G broj bridova maksimalnog sparivanja jednak je broju vrhova minimalnog pokrivača, tj. vrijedi jednakost \upsilon (G)=\tau(G).
Definicija 15. Kažemo da bipartitni graf G(X,Y) ima potpuno sparivanje u X ako postoji sparivanje u Gkoje zasićuje sve vrhove iz X.
Potpuno sparivanje, dakle, definira jedno 1-1 preslikavanje između vrhova iz X i jednog dijela vrhova iz Y koje odgovarajuće vrhove iz X i Y spaja bridom. Stoga za svakih k vrhova iz X mora postojati barem k njima susjednih vrhova u Y. To je, dakle, nuždan uvjet za postojanje potpunog sparivanja. Sljedeći teorem kazuje da je to i dovoljan uvjet.
Teorem 16.[P. Hall, 1935.] Bipartitni graf G s biparticijom (X,Y) ima potpuno sparivanje ako i samo ako za svaki S\subseteq X vrijedi Hallov uvjet:
\left\vert N\left( S\right) \right\vert \geq\left\vert S\right\vert ,
gdje je N(S)\subseteq Y skup svih vrhova grafa G koji su susjedni vrhovima iz S.Ako particije X i Y imaju jednak broj elemenata, onda su potpunim sparivanjem u X zasićeni i svi vrhovi iz Y, pa je riječ o savršenom sparivanju u bipartitnom grafu. O tome govori sljedeći teorem popularno nazvan Teorem o braku.
Teorem 17.[Teorem o braku] Bipartitni graf G s particijom (X,Y) ima savršeno sparivanje ako i samo ako je \left\vert X\right\vert =\left\vert Y\right\vert i \left\vert N(S)\right\vert \geq\left\vert S\right\vert , za svaki S\subseteq X.
Primjenjujući ovaj teorem na uvodne primjere
No, u bipartitnom grafu koji odgovara problemu iz Primjera
2.2Mađarska metoda
Pored samog pitanja egzistencije savršenog sparivanja u bipartitnom grafu, jednako je važno i pitanje njegove konstrukcije u slučaju da takvo sparivanje postoji. Jedna od poznatih metoda koja se bavi pitanjima egzistencije i konstrukcije savršenog sparivanja u bipartitnom grafu je tzv. mađarska metoda. S pomoću nje se ili konstruira savršeno sparivanje u bipartitnom grafu G\left( X,Y\right), ili se pronađe podskup S\subseteq X za koji je \left\vert N\left( S\right) \right\vert \lt \left\vert S\right\vert, pa po Hallovu teoremu slijedi da savršeno sparivanje u G\left( X,Y\right) ne postoji.
Ideja je sljedeća:
Započnemo s nekim sparivanjem M u bipartitnom grafu G\left( X,Y\right), pri čemu za M možemo uzeti i prazan skup ako ne znamo ništa bolje. Ako M zasićuje X, onda je ono i savršeno sparivanje, pa smo gotovi. Ako, pak, postoji M-nezasićen vrh u\in X, onda algoritam sustavno traži M-uvećavajući put P s početkom u vrhu u. Ako takav put postoji, onda za sparivanje M^{\prime}=M\bigtriangleup E\left( P\right), gdje je E\left( P\right) skup bridova puta P, sadržava više bridova i zasićuje više vrhova u X nego sparivanje M. Tako dobivamo veće sparivanje M^{\prime}, a potom cijeli postupak ponovimo tako da umjesto polaznog sparivanja M uzmemo sparivanje M^{\prime }. U slučaju da takav put ne postoji, pronađemo skup R svih vrhova koji su s vrhom u povezani M-alternirajućim putom. Može se pokazati da za skup S=R\cap X vrijedi \left\vert N\left( S\right) \right\vert \lt \left\vert S\right\vert, pa po Hallovu teoremu zaključujemo da ne postoji savršeno sparivanje u bipartitnom grafu G\left( X,Y\right), a po Teoremu
Ovaj algoritam dao je J. Edmonds 1965. godine, a zove se mađarska metoda jer se zasniva na idejama dvojice Mađara: Kőniga i Egerváryja.
Algoritam:
Ulaz. Bipartitni graf G s biparticijom (X,Y), \left\vert X\right\vert =\left\vert Y\right\vert.
Izlaz. Savršeno sparivanje M u G ili skup S\subseteq X za koji je \left\vert N\left( S\right) \right\vert \lt \left\vert S\right\vert.
Korak 1. Neka je M bilo koje sparivanje od G, npr. M=\emptyset.
Korak 2. Ako je XM-zasićen, stop (M je tada savršeno sparivanje od G).
U protivnom, neka je vrh x\in XM-nezasićen.
Stavimo S=\left\lbrace x\right\rbrace ,T=\emptyset.
Korak 3. Ako je N\left( S\right) =T, stop (\left\vert N\left( S\right) \right\vert \lt \left\vert S\right\vert).
U protivnom, neka je y\in N\left( S\right) \setminus T.
Korak 4. Ako je y\in YM-zasićen vrh, neka je zy\in M.
Zamijenimo S sa S\cup\left\lbrace z\right\rbrace, a T sa T\cup\left\lbrace y\right\rbrace i vratimo se na korak 3.
Ako je yM-nezasićen vrh, neka je PM-uvećavajući (x,y)-put.
Zamijenimo M s M\bigtriangleup E\left( P\right) i vratimo se na korak 2.
Pogledajmo kako ovaj algoritam radi na primjeru naših djevojaka i momaka.

Animirani prikaz mađarske metode
Ulaz. Bipartitni graf G(X,Y), X=\left\lbrace D_{1},D_{2},D_{3} ,D_{4}\right\rbrace ,Y=\left\lbrace M_{1},M_{2},M_{3},M_{4}\right\rbrace.
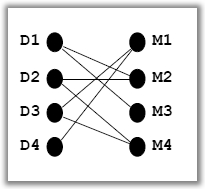
Korak 1. Neka je M=\emptyset.
Korak 2. X nije M-zasićen. Vrh x=D_{1}\in X je M-nezasićen.
Stavimo S=\left\lbrace D_{1}\right\rbrace ,T=\emptyset.
Korak 3. N\left( S\right) =\left\lbrace M_{2},M_{3}\right\rbrace \neq T=\emptyset.
Neka je y=M_{2}\in N\left( S\right) \setminus T=\left\lbrace M_{2},M_{3}\right\rbrace.
Korak 4. y je M-nezasićen vrh. Neka je P=D_{1}M_{2}M-uvećavajući put.
\qquad\qquad M=\left\lbrace D_{1}M_{2}\right\rbrace i vratimo se na korak 2.
Korak 2. X je M=\left\lbrace D_{1}M_{2}\right\rbrace-nezasićen. Vrh x=D_{2}\in X je M-nezasićen.
Stavimo S=\left\lbrace D_{2}\right\rbrace ,T=\emptyset.
Korak 3. N\left( S\right) =\left\lbrace M_{2},M_{4}\right\rbrace \neq T=\emptyset.
Neka je y=M_{2}\in N\left( S\right) \setminus T=\left\lbrace M_{2},M_{4}\right\rbrace.
Korak 4. y=M_{2} je M-zasićen vrh jer je D_{1}M_{2}\in M.
S=S\cup\left\lbrace D_{1}\right\rbrace =\left\lbrace D_{1} ,D_{2}\right\rbrace ,T=T\cup\left\lbrace M_{2}\right\rbrace =\left\lbrace M_{2}\right\rbrace
Vratimo se na korak 3.
Korak 3. N\left( S\right) =N\left( \left\lbrace D_{1},D_{2}\right\rbrace \right) =\left\lbrace M_{2},M_{3},M_{4}\right\rbrace \neq T=\left\lbrace M_{2}\right\rbrace
Neka je y=M_{3}\in N\left( S\right) \setminus T=\left\lbrace M_{3},M_{4}\right\rbrace
Korak 4. y=M_{3} je M-nezasićen.
Neka je P=D_{2}M_{2}D_{1}M_{3}M-uvećavajući (D_{2},M_{3})-put.
M=M\vartriangle E\left( P\right) =\left\lbrace D_{1} M_{3},D_{2}M_{2}\right\rbrace i vratimo se na korak 2.
Korak 2. X jeM=\left\lbrace D_{1}M_{3},D_{2}M_{2}\right\rbrace-nezasićen.
Vrh x=D_{3}\in X je M-nezasićen.
Stavimo S=\left\lbrace D_{3}\right\rbrace ,T=\emptyset.
Korak 3. N\left( S\right) =\left\lbrace M_{1},M_{4}\right\rbrace \neq T=\emptyset.
Neka je y=M_{1}\in N\left( S\right) \setminus T=\left\lbrace M_{1},M_{4}\right\rbrace.
Korak 4. y=M_{1} je M-nezasićen vrh.
P=D_{3}M_{1} je M-uvećavajući (D_{3},M_{1} )-put, E\left( P\right) =\left\lbrace D_{3}M_{1}\right\rbrace
M=M\vartriangle E\left( P\right) =\left\lbrace D_{1} M_{3},D_{2}M_{2},D_{3}M_{1}\right\rbrace i vratimo se na korak 2.
Korak 2. X je M=\left\lbrace D_{1}M_{3},D_{2}M_{2},D_{3}M_{1}\right\rbrace-nezasićen.
Vrh x=D_{4}\in X je M-nezasićen.
Stavimo S=\left\lbrace D_{4}\right\rbrace ,T=\emptyset.
Korak 3. N\left( S\right) =\left\lbrace M_{1}\right\rbrace \neq T=\emptyset.
Neka je M_{1}\in N\left( S\right) \setminus T=\left\lbrace M_{1}\right\rbrace.
Korak 4. y=M_{1} je M-zasićen vrh jer je D_{3}M_{1}\in M.
S=S\cup\left\lbrace D_{3}\right\rbrace =\left\lbrace D_{3} ,D_{4}\right\rbrace ,T=T\cup\left\lbrace M_{1}\right\rbrace =\left\lbrace M_{1}\right\rbrace
Vratimo se na korak 3.
Korak 3. N\left( S\right) =N\left( \left\lbrace D_{3},D_{4}\right\rbrace \right) =\left\lbrace M_{1},M_{4}\right\rbrace \neq T=\left\lbrace M_{1}\right\rbrace
Neka je y=M_{4}\in N\left( S\right) \setminus T=\left\lbrace M_{4}\right\rbrace
Korak 4. y=M_{4} je M-nezasićen.
P=D_{4}M_{1}D_{3}M_{4} je M-uvećavajući (D_{4},M_{4})-put, E\left( P\right) =\left\lbrace D_{4}M_{1},D_{3}M_{1} ,D_{3}M_{4}\right\rbrace,
M=M\vartriangle E\left( P\right) =\left\lbrace D_{1} M_{3},D_{2}M_{2},D_{3}M_{4},D_{4}M_{1}\right\rbrace,
vratimo se na korak 2.
Korak 2. X je M=\left\lbrace D_{1}M_{3},D_{2}M_{2},D_{3}M_{4},D_{4} M_{1}\right\rbrace-zasićen, pa smo gotovi.
M je savršeno sparivanje.
Primijetimo da nam Mađarska metoda daje samo egzistenciju jednog savršenog sparivanja, no ne kaže nam ništa o broju svih mogućih savršenih sparivanja. U praksi nam može biti od važnosti poznavati njihov broj. O tome više u sljedećem poglavlju.
3Prebrojavanje Kekuléovih struktura
U daljnjem ćemo tekstu najviše pozornosti posvetiti molekularnim grafovima, pa ćemo se za savršena sparivanja koristiti izraz Kekuléove strukture. Kekuléove strukture igraju posebno važnu ulogu u proučavanju benzenoida. Benzenoidni graf je povezani graf čije se ravninsko smještanje sastoji od kongruentnih pravilnih šesterokuta, tako da svaka dva šesterokuta ili imaju zajednički vrh, ili su disjunktni. U literaturi ih ponekad nazivaju i poliheksi, heksagonalne životinje, heksagonalna poliomina, heksagonalni sustavi i sl. Za benzenoid kažemo da je katakondenziran ako nijedan vrh nije incidentan s tri šesterokuta. Za benzenoid kažemo da je benzenoidni lanac ako je katakondenziran i nijedan šeterokut nema tri susjedna šesterokuta. Prebrojavanje savršenih sparivanja ima važne kemijske primjene. Naime, Linus Pauling (dobitnik dviju Nobelovih nagrada) uočio je da se s pomoću Paulingova reda veze (omjer broja Kekuléovih struktura koje udvostručavaju neku vezu i svih Kekuléovih struktura) može izračunati aproksimacija duljine veze među atomima ugljika u benzenoidnim molekulama.
3.1Linearne rekurzivne metode
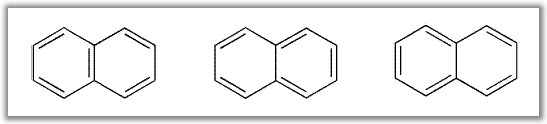
Označimo s G neki molekularni graf, a sa k podgraf koji čini Kekuléovu strukturu, tj. koji se sastoji od nesusjednih bridova grafa G, a svaki vrh grafa G je incidentan s točno jednim bridom u k. Naprimjer, za naftalen se mogu pronaći tri Kekuléove strukture.
S K\left( G\right) označimo broj svih različitih Kekuléovih struktura u grafu G. Da bismo odredili taj broj poslužit ćemo se linearnim rekurzijama na grafu i njegovim podgrafovima. Od samih početaka pa sve do danas, metode za prebrojavanje Kekuléovih struktura temelje se upravo na takvim rekurzijama.
Neka je e proizvoljan brid grafa G. S G-e označimo graf koji se dobije iz grafa G kada mu uklonimo brid e, a s G\circleddash e graf koji se dobije iz grafa G uklanjanjem brida e i svih njemu susjednih bridova. Tada vrijedi jednostavna rekurzija
(1)
K(G)=K(G-e)+K(G\circleddash e)
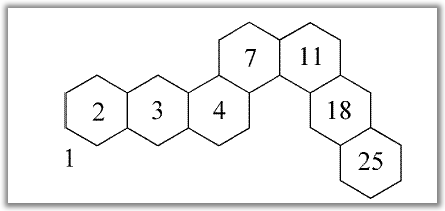
| (1) | U šesterokute grafa koji prikazuje katakondenzirani benzenoidni lanac upisuju se brojevi počevši od jednog kraja i to na način: izvan početnog šesterokuta upiše se broj 1, a u prvi šesterokut upiše se broj 2. |
| (2) | Svaki broj u ostalim šesterokutima dobije se kao suma onog broja koji je upisan u šesterokut koji je njegov direktni prethodnik (njih dva određuju smjer) i onog koji je upisan u šesterokut neposredno prije skretanja lanca u tom smjeru. |
| (3) | Broj koji je upisan u zadnji šesterokut lanca upravo je broj Kekuléovih struktura K(G). |
U našem primjeru je K(G)=25.
3.2Metode transfer matrice
Linearna rekurzija K(G)=K(G-e)+K(G\circleddash e) u slučaju grafova polimera (lanac s mnogo ponavljajućih elemenata — ponavljajuće elemente nazivamo monomerima) ima vrlo elegantan oblik bez obzira na to kakvi su polimeri u pitanju. Mi ćemo se ovdje fokusirati na regularne polimere u kojima se ponavlja ista jedinica monomera. Broj Kekuléovih struktura K_{L} za ciklički lanac polimera duljine L se može izraziti u obliku
K_{L}=tr\left( \rho\cdot T^{L}\right)
gdje je T transfer matrica karakteristična za jedinicu određenog monomera, a \rho matrica koja opisuje karakter rubnih uvjeta, npr. krajeva lanca polimera. Iz matrice T vidljivi su svi različiti načini na koje se Kekuléove strukture mogu načiniti iz jednog uzorka na granici jedne jedinice monomera do drugog uzorka na granici sljedeće jedinice monomera.
Primjer 18. Nađimo transfer matricu za lanac polifena dug 14 heksagona.
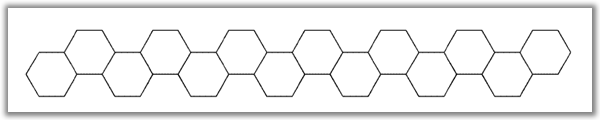
Taj lanac može se podijeliti na ćelije monomera kao na slici.

S obzirom na vertikalnu os simetrije ovih šesterokuta razlikujemo lijevi i desni monomer. S lijeve i desne strane osi simetrije je neparan broj vrhova šesterokuta (3), pa moramo imati i neparan broj dvostrukih bridova (bridova u sparivanju) koji sijeku os simetrije. Budući da samo dva lijeva brida sijeku os simetrije, točno je jedan od njih dvostruki brid. Sve mogućnosti za postavljanje dvostrukih veza na granici monomera prikazane su na sljedećoj slici.

U slučaju da je gornji lijevi brid koji siječe os simetrije dvostruki brid, postoje dva načina za nastavak na sljedećoj granici, dok se u slučaju donjeg lijevog dvostrukog brida može nastaviti samo na jedan način jer propada mogućnost donja lijeva dvostruka veza\rightarrow gornja desna dvostruka veza. Naime, ta nas mogućnost dovodi do nezasićenog vrha (vidite donju sliku). Vrhove A i B ne smijemo spojiti dvostrukim bridom jer već imamo jednu dvostruku vezu koja siječe os simetrije, a znamo da može biti samo jedna takva. To znači da vrh B ostaje nezasićen, pa ta mogućnost ne daje savršeno sparivanje.
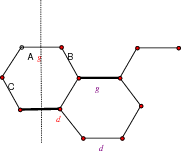
Dakle, transfer matrica je oblika
\begin{bmatrix} g\rightarrow g & g\rightarrow d\\ d\rightarrow g & d\rightarrow d \end{bmatrix} \Rightarrow T= \begin{bmatrix} 1 & 1\\ 0 & 1 \end{bmatrix}.
Za uske lance (široke par šesterokuta) postoji tek nekoliko mogućih uzoraka, tako da je matrica T malog reda, a nakon njene dijagonalizacije lako se izračuna i tražena potencija matrice T za proizvoljnu duljinu lanca L. No, s povećanjem širine trake w, tj. broja veza koje presijecaju os simetrije, eksponencijalno se povećava i red matrice T, ali ova tehnika sigurno je primjenjiva za širine w\leq 12.
Primjer 19. Odredimo transfer matrice za lanac prikazan na donjoj slici.
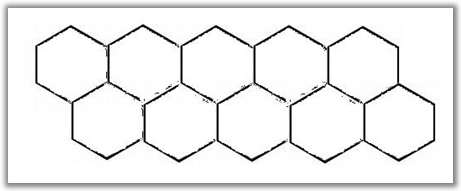

Lijevo od osi simetrije imamo neparan broj vrhova šesterokuta (ima ih 5), pa moramo imati i neparan broj dvostrukih bridova (bridova u sparivanju) koji sijeku os simetrije. Dakle, imamo jedan ili tri dvostruka brida koja sijeku os simetrije. Ispitajmo svaku mogućnost zasebno. Najprije pogledajmo sve mogućnosti u kojima je samo gornji lijevi brid dvostruki:



Očito, sve tri mogućnosti zasićuju sve vrhove, tj. vode do savršenog sparivanja.
Mogućnost srednja lijeva dvostruka veza\rightarrow gornja desna dvostruka veza nije dobra (slika
Ostale dvije mogućnosti (slika
Sljedeće mogućnosti počinju s donjim lijevim dvostrukim bridom. U prva dva slučaja (slika
donja lijeva dvostruka veza\rightarrow gornja desna dvostruka veza i donja lijeva dvostruka veza\rightarrow srednja desna dvostruka veza nije moguće savršeno sparivanje jer dobivamo nezasićene vrhove (vrh A), dok je situacija donja lijeva dvostruka veza\rightarrow donja desna dvostruka veza u redu.
I napokon, ako su sva tri lijeva brida koja sijeku os simetrije dvostruki bridovi (slika
Dakle, transfer matrica je oblika
\begin{bmatrix} g\rightarrow g & g\rightarrow s & g\rightarrow d & g\rightarrow gsd\\ s\rightarrow g & s\rightarrow s & s\rightarrow d & s\rightarrow gsd\\ d\rightarrow g & d\rightarrow s & d\rightarrow d & d\rightarrow gsd\\ gsd\rightarrow g & gsd\rightarrow s & gsd\rightarrow d & gsd\rightarrow gsd \end{bmatrix} \Rightarrow T= \begin{bmatrix} 1 & 1 & 1 & 0\\ 0 & 1 & 1 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 \end{bmatrix},
što možemo poistovjetiti s matricom reda 3 oblika
T= \begin{bmatrix} 1 & 1 & 1\\ 0 & 1 & 1\\ 0 & 0 & 1 \end{bmatrix}.
Lako se provjeri da je
T^{n}= \begin{bmatrix} 1 & n & \frac{n\left( n+1\right) }{2}\\ 0 & 1 & n\\ 0 & 0 & 1 \end{bmatrix},
pa dobivamo broj Kekuléovih struktura u lancu duljine L u eksplicitnom obliku
K_{L}=3+2L+\frac{1}{2}L\left( L+1\right).
Uočimo da je ova eksplicitna jednadžba analogna linearnoj rekurziji
p\left( x\right) =\det\left( xI-T\right) =-\sum_{i=0}^{n}a_{i}x^{n-i},
onda je, po Hamilton-Cayleyevu teoremu, T^{n}=\sum\limits_{i=1}^{n} a_{i}T^{n-i}, pa je
K_{L+1}=tr\left( \rho\cdot T^{L+1-n}\cdot T^{n}\right) =\sum_{i=1}^{n} a_{i}tr\left( \rho\cdot T^{L+1-i}\right) =\sum\limits_{i=1}^{n} a_{i}K_{L+1-i},
što je prvobitna linearna rekurzija
Za naš primjer strukture polifena je K_{L+1}=K_{L}+K_{L-1}. Primijetimo da je rekurzija uvelike neovisna o krajevima lanca, ali oni utječu na početne vrijednosti na kojima se rekurzija temelji.
Bibliografija