Regularni politopi
Sažetak
U ovom članku promatramo dvodimenzionalne, trodimenzionalne i višedimenzionalne regularne politope. Pozabavili smo se ponajprije njihovom egzistencijom, konstrukcijom te svojstvima koja zadovoljavaju njihovi elementi. Najvažniji teorem članka, poznat pod nazivom Euler–Poincaréova formula, nalazi se u šestom poglavlju te povezuje broj svih elemenata n–dimenzionalnog politopa.
Sadržaj
1Uvod
Teorija politopa u dvodimenzionalnom i trodimenzionalnom Euklidskom prostoru jedna je od najstarijih grana matematike. Još od antičkih vremena bila je intrigantno područje tadašnjim matematičarima pa su tako regularni poligoni i poliedri činili znatan dio njihovih proučavanja. Pretpostavlja se da su čak i pitagorejci bili upoznati s regularnim poliedrima.
Osoba koja je prva sustavno iznijela teoriju regularnih poliedara bio je Euklid. U XIII. knjizi „Elemenata”, posvećenoj upravo regularnim poliedrima, Euklid, uz njihovu definiciju, daje dokaz njihove egzistencije, konstrukcije pa i dokaz da ih postoji samo pet. Zbog algebarskih, geometrijskih i kombinatornih svojstava koja regularni poliedri imaju, matematičari su često pokušavali naći njima analogne objekte koji bi imali neka, ne nužno sva, svojstva regularnih poliedara. Međutim, bilo je potrebno duže razdoblje da bi se stvorili preduvjeti za daljnji razvoj ovog područja matematike pa je tek u 19. stoljeću dokazano da postoje n–dimenzionalni politopi, n \geq 4. U trenutku kada je Ludwig Schäfli dokazao da takvi objekti postoje, tek je nekolicina matematičara bila svjesna da je geometrija u n–dimenzionalnom prostoru, n \geq 4, moguća. Također je pokazano da su jedini regularni politopi u tim prostorima poopćenja određenih regularnih poliedara. Premda su regularni politopi uglavnom proučavani radi svojeg oblika, a prvobitna im je upotreba bila u umjetnosti, danas imaju i praktičnu primjenu u mineralogiji, arhitekturi, linearnom programiranju i drugim područjima.
Temeljna ideja članka je upoznati čitatelja s osnovnim pojmovima iz teorije regularnih politopa te se nadamo da ćemo nekoga potaknuti da sazna više o ovoj temi. Naše putovanje kroz dimenzije počinjemo od najmanjih:
2Manje dimenzije
U 0–dimenzionalnom prostoru jedini objekti su točke dok u jednodimenzionalnom imamo i dužine. Iz sljedeće definicije vidimo da je 2–dimenzionalni prostor nešto bogatiji.
Definicija 1. Poligon je konačno područje omeđeno s p\geq 3 dužina \overline{A_{1}A_{2}}, \overline{A_{2}A_{3}}, \ldots, \overline{A_{p}A_{1}} koje se ne sijeku osim u zajedničkom vrhu, ako takav postoji.
Definicija 2. Ćelija poligona \pi_{2} je brid danog poligona.
Definicija 3. Vršna figura vrha V poligona \pi_{2} je dužina čije su krajnje točke polovišta bridova incidentnih s vrhom V.
Posebnu klasu poligona čine regularni poligoni:
Definicija 4. Poligon je regularan ako su svi njegovi bridovi i svi unutrašnji kutovi sukladni.
L. Schläfli uveo je notaciju regularnih politopa koja se njemu u čast naziva Schläflijev simbol. U kontekstu Schläflijeve notacije, regularne poligone s p stranica, odnosno p–terokute, označavamo s \left\lbrace p \right\rbrace. Laganim računom dobivamo da su mjere unutrašnjih kutova \left\lbrace p \right\rbrace–a jednake
\displaystyle\frac{ \left( p-2 \right) \cdot 180^{\circ}}{p}. Primjenom teorema SKS o sukladnosti trokuta na jednakokračne trokute čiji je jedan vrh vrh \left\lbrace p \right\rbrace–a, a osnovica vršna figura tog vrha, dobivamo da su vršne figure \left\lbrace p \right\rbrace–a sukladne.
Regularnih poligona ima beskonačno mnogo, za razliku od njihovih višedimenzionalnih poopćenja.
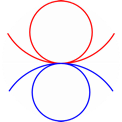
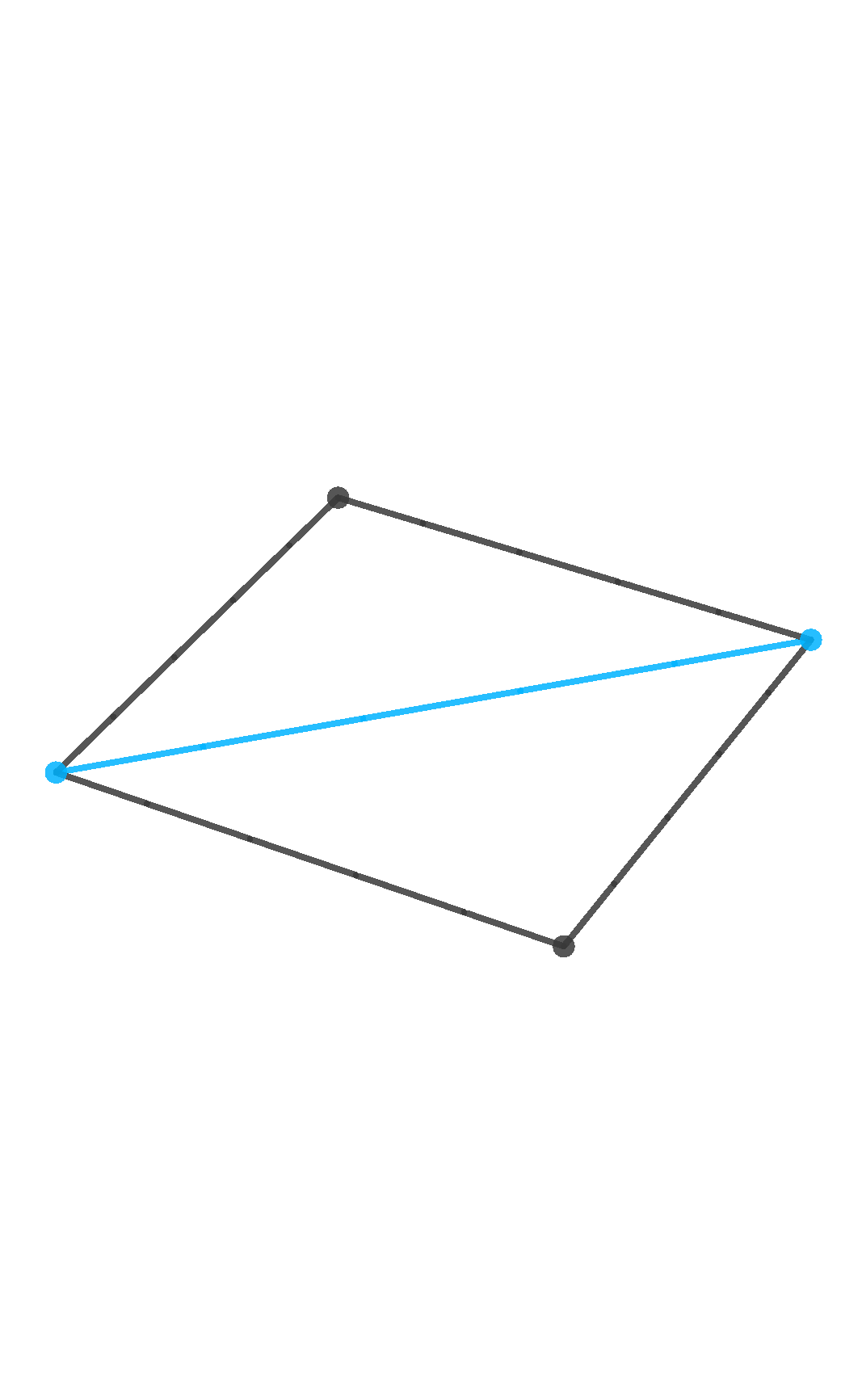
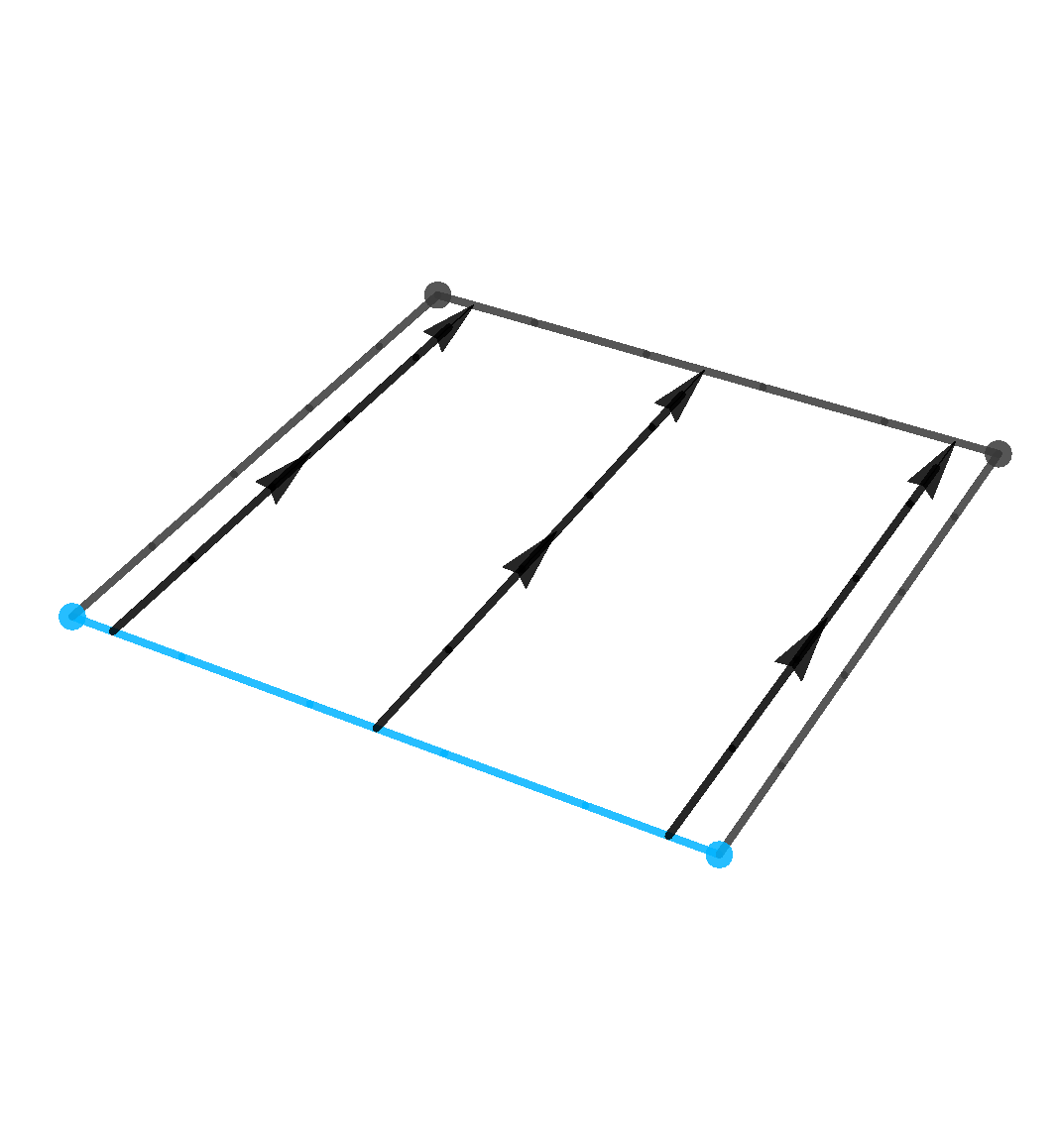
Definicija 5. Dualan poligon danog poligona \pi_{2} je poligon čiji su vrhovi polovišta bridova od \pi_{2}.
Definicija 6. Okrnjen poligon danog poligona \pi_{2} je poligon čiji su bridovi vršne figure vrhova od \pi_{2}.
Napomena 7. Primijetimo da je \pi'_{2} okrnjen poligon poligona \pi_{2} ako i samo ako je \pi'_{2} dualan poligon poligonu \pi_{2}. Prethodna tvrdnja slijedi iz definicije, ali ona neće vrijediti u višim dimenzijama.
Na sljedećoj se slici vidi što se događa u slučaju kvadrata:
3Kroz poznato...
U ovom ćemo se poglavlju upoznati s trodimenzionalnim tijelima te nekim njihovim svojstvima. Počnimo s definicijom:
Definicija 8. Poliedar je konačan skup poligona tako raspoređenih u prostoru da je svaki brid nekog poligona ujedno brid još točno jednog poligona.
Definicija 9. Svaki od poligona iz prethodne definicije nazivamo ćelijom danog poliedra \pi_{3}.
Definicija 10. Vršna figura vrha V poliedra \pi_{3} je poligon čije su krajnje točke polovišta bridova incidentnih s vrhom V.
Definicija 11. Poliedar je regularan ako su njegove ćelije i vršne figure regularni poligoni.
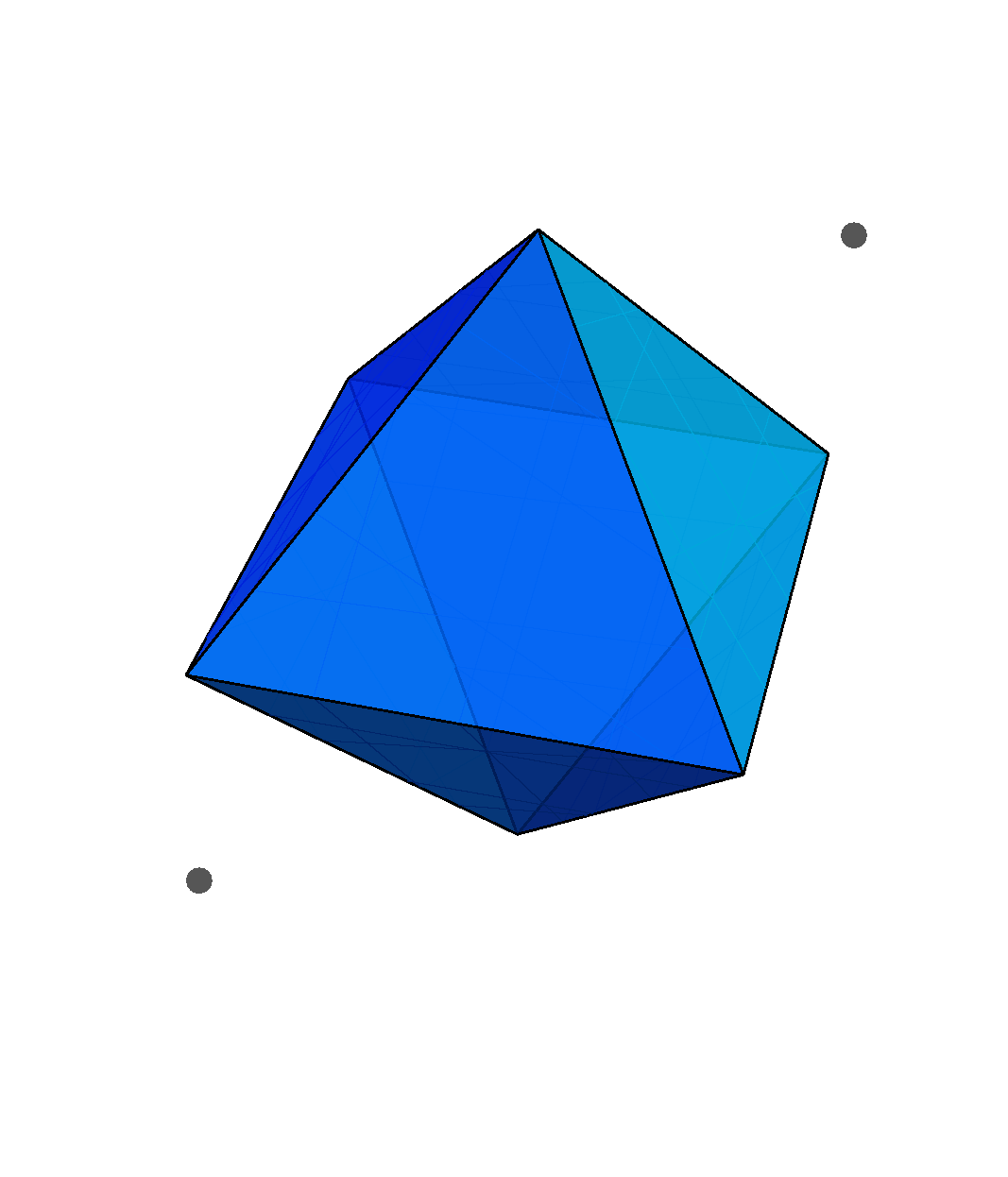
Schläflijev simbol regularnog poliedra je \left\lbrace p,q \right\rbrace pri čemu je \left\lbrace p \right\rbrace ćelija, a \left\lbrace q \right\rbrace vršna figura danog poliedra. Na slici
U poliedru \pi_{3} označimo broj vrhova s N_{0} , broj bridova s N_{1} te broj strana s N_{2}. Imajući u vidu ove oznake, vrijedi sljedeći, važan rezultat:
Teorem 12. (Eulerova formula) Za konveksan \pi_{3} vrijedi
N_{0}-N_{1}+N_{2}=2.
Dokaz. Neka je \phi=N_{0}-N_{1}+N_{2}-1. Treba dokazati da je \phi=1. Promatramo konstrukciju poliedra. U prvom koraku imamo jednu stranicu. Dakle, tada je
U nekom koraku konstrukcije dodajemo k–terokut koji ima l zajedničkih bridova s dosadašnjom konstrukcijom, to jest l+1 zajedničkih vrhova. Označimo li s N_{2}, N_{1} i N_{0} broj strana, bridova i vrhova konstruiranog objekta prije dodavanja k–terokuta respektivno, te analogno N'_{2}, N'_{1}, N'_{0} nakon dodavanja k–terokuta, dobivamo sljedeći niz jednakosti:
U zadnjem koraku konstrukcije broj vrhova i bridova se ne mijenja, dok se broj strana poveća za 1 pa vrijedi:
N_{2}=1, N_{0}=N_{1}=:n \Longrightarrow \phi=0.
Dodajemo poligone na dosadašnju konstrukciju tako da imaju barem jedan zajednički brid. Indukcijom pokazujemo da, sve dok ne dobijemo „potpuni” poliedar, vrijedi \phi=0.U nekom koraku konstrukcije dodajemo k–terokut koji ima l zajedničkih bridova s dosadašnjom konstrukcijom, to jest l+1 zajedničkih vrhova. Označimo li s N_{2}, N_{1} i N_{0} broj strana, bridova i vrhova konstruiranog objekta prije dodavanja k–terokuta respektivno, te analogno N'_{2}, N'_{1}, N'_{0} nakon dodavanja k–terokuta, dobivamo sljedeći niz jednakosti:
\begin{align*} N'_{0} &= N_{0}+k-l-1,\\ N'_{1} &= N_{0}+k-1,\\ N'_{2} &= N_{0}+1. \end{align*}
Dakle, \phi'=N'_{0}-N'_{1}+N'_{2}-1=N_{0}-N_{1}+N_{2}-1=\phi=0.U zadnjem koraku konstrukcije broj vrhova i bridova se ne mijenja, dok se broj strana poveća za 1 pa vrijedi:
\left. \begin{aligned} N'_{0} &= N_{0} \\ N'_{1} &= N_{1} \\ N'_{2} &= N_{2}+1 \end{aligned} \right\rbrace \Longrightarrow\phi'=1.
\ \blacksquare
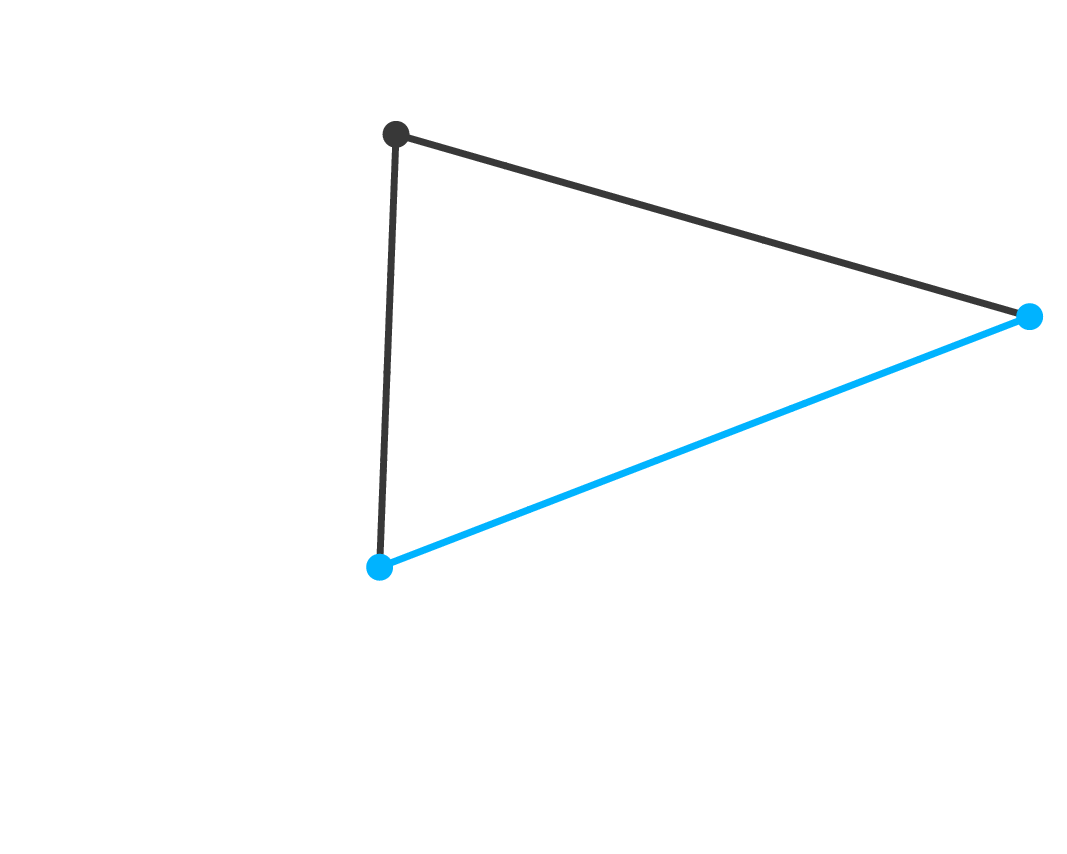
U sljedećem teoremu upotrebljavamo pojmove prizma, piramida i antiprizma, od kojih definiramo, ne sasvim precizno, samo posljednji. Poznato je na koji način možemo točku i \left\lbrace p \right\rbrace spojiti s p trokuta kako bismo formirali piramidu. Također je jasno da spajanjem dvaju sukladnih \left\lbrace p \right\rbrace pravokutnicima dobivamo prizmu. Na slici
Antiprizma je poliedar sastavljen od dvaju sukladnih paralelnih poligona (baza) tako postavljenih u prostoru da ih možemo povezati nizom „alternirajućih” trokuta. Kažemo da je antiprizma p–strana ako su njene baze \left\lbrace p \right\rbrace. Primjer šesterostrane i sedmerostrane antiprizme ilustrirani su slikom
Teorem 13. Postoji 5 Platonovih tijela do na sličnost.
Dokaz. Neka je dan poliedar \left\lbrace m,n \right\rbrace. Očito je da vrijedi 2N_{1}=mN_{2}=nN_{0}. Koristeći se Eulerovom formulom dobivamo:
Time smo pokazali da nema više od 5 Platonovih tijela. Konstrukcijom ćemo pokazati da zaista sva i postoje. \left\lbrace 3,3 \right\rbrace je piramida čija baza je trokut, \left\lbrace 4,3 \right\rbrace je prizma čija je baza kvadrat,
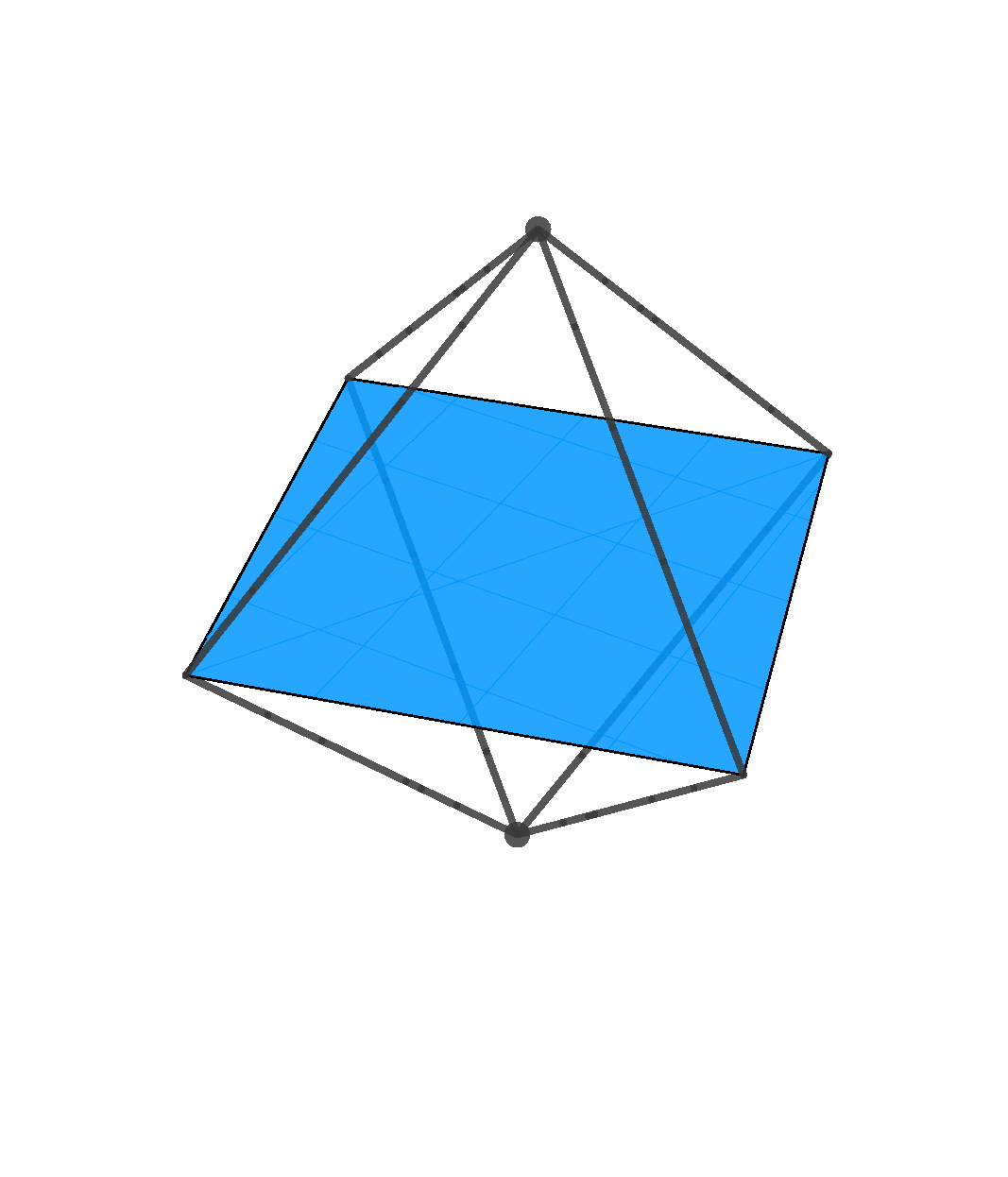
\left\lbrace 3,4 \right\rbrace dobivamo spajanjem dviju pravilnih četverostranih piramida tako da im se baze poklapaju ( vidi sliku 6 ).
\left\lbrace 3,5 \right\rbrace dobivamo spajanjem dviju pravilnih peterostranih piramida i jedne peterostrane antiprizme, kako je i prikazano na slici 7 .
Preostaje opisati konstrukciju \left\lbrace 5,3 \right\rbrace–na odgovarajući način spojimo 6 peterokuta kako bismo formirali „zdjelu”. Slobodni bridovi čine deseterokut koji ne leži u ravnini. Spajanjem dvaju takvih objekata duž spomenutih slobodnih bridova dobivamo \left\lbrace 5,3 \right\rbrace.
Gornju konstrukciju možete vidjeti na slici 8 .
\begin{align*} 2\frac{N_{1}}{m}-N_{1}+2\frac{N_{1}}{n} &= 2 \\ 2nN_{1}-mnN_{1}+2mN_{1}&= 2mn \\ N_{1} \left( 2n-mn+2m \right)&= 2mn. \end{align*}
Ta jednakost vrijedi samo ako je 2n-mn+2m\gt 0 , to jest mn-2n-2m+4\lt 4 , odnosno ako je \left( m-2 \right) \left( n-2 \right) \lt 4. Dakle, \left( m-2 \right) \left( n-2 \right) \in \left\lbrace 1,2,3 \right\rbrace. Razlikujemo tri slučaja:
| (1) | \left( m-2 \right) \left( n-2 \right) =1\Longrightarrow m=n=3 |
| (2) | \left( m-2 \right) \left( n-2 \right) =2\Longrightarrow \left( m,n \right) \in \left\lbrace \left( 3,4 \right) , \left( 4,3 \right) \right\rbrace |
| (3) | \left( m-2 \right) \left( n-2 \right) =3\Longrightarrow \left( m,n \right) \in \left\lbrace \left( 3,5 \right) , \left( 5,3 \right) \right\rbrace. |
\ \blacksquare
U tablici
| Naziv | Element | Schläflijev simbol | N_{0} | N_{1} | N_{2} |
| Tetraedar | vatra | \left\lbrace 3,3 \right\rbrace | 4 | 6 | 4 |
| Oktaedar | zrak | \left\lbrace 3,4 \right\rbrace | 6 | 12 | 8 |
| Kocka | zemlja | \left\lbrace 4,3 \right\rbrace | 8 | 12 | 6 |
| Ikozaedar | voda | \left\lbrace 3,5 \right\rbrace | 12 | 30 | 20 |
| Dodekaedar | svemir | \left\lbrace 5,3 \right\rbrace | 20 | 30 | 12 |
Pogledajmo na primjeru ikozaedra što predstavlja Schläflijev simbol te što su pripadne vršne figure i ćelije. Schläflijev simbol ikozaedra je \left\lbrace 3,5 \right\rbrace, što po definiciji znači da su ćelije trokuti (jasno, regularni), a vršne figure peterokuti (također regularni), kao što se može uočiti na već prije spomenutoj slici
Definicija 14. Dualan poliedar poliedra \pi_{3} je onaj poliedar čiji su vrhovi težišta ćelija poliedra \pi_{3}.
Definicija 15. Okrnjen poliedar poliedra \pi_{3} je onaj poliedar čije su ćelije vršne figure od \pi_{3} i okrnjeni poligoni ćelija od \pi_{3}.
Na primjerima ćemo vidjeti što su to dualni i okrnjeni poliedri. Odmah je jasno da je tetraedar dualan sam sebi. Oktaedar i kocka su međusobno dualni te su isto tako dodekaedar i ikozaedar međusobno dualni. Navedeno možete vidjeti na slikama
Slika 10: Dual tetraedra & dualnost \left\lbrace 3,4 \right\rbrace \leftrightarrow \left\lbrace 4,3 \right\rbrace
Iz definicije je jasno, uz gornju napomenu, da je okrnjen poligon regularnog poligona regularan. No, okrnjen poliedar regularnog poliedra ne mora nužno biti regularan. Npr. strane okrnjene kocke su trokuti – kao vršne figure kocke, i kvadrati – okrnjeni poligoni strana kocke. Takvo tijelo ne može biti regularno. S druge strane, okrnjen tetraedar je oktaedar.
Slika
4... generalizacijom...
Definicija 16. Za skup točaka S u n–dimenzionalnom prostoru kažemo da je konveksan ako za svake dvije točke x,y\in S vrijedi \left[ x,y \right] \subseteq S , pri čemu je
\left[ x,y \right] = \left\lbrace y+ \left( x-y \right) \lambda \ |\ \lambda \in \left[ 0,1 \right] \right\rbrace.
\left[ x,y \right] = \left\lbrace y+ \left( x-y \right) \lambda \ |\ \lambda \in \left[ 0,1 \right] \right\rbrace.
Definicija 17. Za skup točaka S\subseteq E^{n} definiramo njegov konveksan zatvarač \bar{S} kao presjek svih konveksnih nadskupova od S:
\bar{S}=\bigcap_{\substack{S\subseteq\mathcal{K}\\\mathcal{K}\text{ konveksan}}}\mathcal{K}.
Napomena 18. Presjek konveksnih skupova je konveksan skup pa je i konveksan zatvarač konveksan. Primijetimo da je konveksan zatvarač najmanji konveksan skup koji sadržava polazni skup.
Definicija 19. Neka su a_{0},a_{1},\ldots,a_{n}\in\mathbb{R}. Skup svih točaka n–dimenzionalnog prostora koje zadovoljavaju jednakost
a_{1}x_{1}+a_{2}x_{2}+\ldots+a_{n}x_{n}=a_{0}
nazivamo hiperravninom.
Napomena 20. Za n=2 uobičajen naziv je pravac, a za n=3 jednostavno ravnina.
Definicija 21. Politop je ograničeno konveksno područje n\ - dimenzionalnog prostora omeđeno s konačno mnogo hiperravnina. Neprazan presjek politopa i hiperravnine nazivamo ćelijom.
Uočimo da je ćelija n–dimenzionalnog politopa \left( n-1 \right)–dimenzionalni politop.
Napomena 22. Politop za n=2 je poligon, a za n=3 je poliedar.
Definicija 23. Vršna figura vrha V politopa \pi_{n} u n–dimenzionalnom prostoru je
\left( n-1 \right)–dimenzionalni politop čiji su vrhovi ona polovišta bridova politopa \pi_{n} koji su incidentni s vrhom V.
\left( n-1 \right)–dimenzionalni politop čiji su vrhovi ona polovišta bridova politopa \pi_{n} koji su incidentni s vrhom V.
Definicija 24. Neka je \pi_{k}^{1}, \pi_{k}^{2}, \ldots, \pi_{k}^{n_{k}} proizvoljan odabir k–dimenzionalnih politopa. Formalnu sumu
\sum_{j=1}^{n_{k}}x_{j}\pi_{k}^{j},
gdje je svaki x_{j}\in \left\lbrace 0,1 \right\rbrace , nazivamo k–lancem. Suma ćelija \pi_{k} je k–lanac koji nazivamo rub politopa \pi_{k+1}.Za dva k–lanca \sum_{j=1}^{n_{k}}x_{j}\pi_{k}^{j} , \sum_{j=1}^{m_{k}}y_{j}\lambda_{k}^{j} definiramo njihovu sumu kao lanac \sum_{j=1}^{M}z_{j}\mu_{k}^{j} , gdje je M=\max \left\lbrace n_{k},m_{k} \right\rbrace. Nadalje je
\mu_{k}^{j}\in \Pi \cup \Lambda,\quad \Pi= \left\lbrace \pi_{k}^{j}\ |\ 1\leq j \leq n_{k} \right\rbrace ,\ \Lambda= \left\lbrace \lambda_{k}^{j}\ |\ 1\leq j \leq m_{k} \right\rbrace .
Neka su indeksi l_{1} \text{ i } l_{2} takvi da je \mu_{k}^{j}=\pi_{k}^{l_{1}}=\lambda_{k}^{l_{2}}. Ako takvi ne postoje, stavimo x_{l_{1}}=0 odnosno y_{l_{2}}=0. Za koeficijente z_{j} vrijedi
z_{j}=0 \Longleftrightarrow x_{l_{1}}=y_{l_{2}}.
Rub k–lanca stoga možemo definirati kao sumu rubova politopa koji čine taj lanac. Jasno je da će tada rub politopa \pi_{k+1} biti k–lanac čiji rubni \left( k-1 \right)–lanac „nestaje” (svi koeficijenti x_{j} iz definicije su 0). Takav k–lanac nazivamo k–mreža.
Definicija 25. Jednostavno povezan politop \pi_{n} je onaj čija je svaka k–mreža rub nekog \left( k+1 \right)–lanca.
Definicija 26. Kažemo da je politop \pi_{n}, n\gt 2 regularan ako su njegove ćelije i vršne figure regularne.
Napomena 27. Regularan politop je jednostavno povezan.
Očito je da su sve ćelije regularnog politopa sukladne, a može se pokazati da isto vrijedi i za vršne figure.
Definicija 28. Neka je dan politop \pi_{n} s k\left( n-1 \right)–dimenzionalnih ćelija. Označimo li s T_{1}, \ldots, T_{k} težišta tih ćelija, tada je sljedećom relacijom definiran njemu dualan politop \overline{\pi}_{n} :
\overline{\pi}_{n}=\overline{ \left\lbrace T_{1}, \ldots, T_{k} \right\rbrace }.
Definicija 29. Okrnjen politop politopa \pi_{n},\ n\gt 2 je onaj čiji rub čine vršne figure od \pi_{n} te okrnjeni politopi koji čine rub od \pi_{n}.
Schläflijev simbol regularnog politopa \pi_{n} u n–dimenzionalnom prostoru, n\gt 2 , označavamo s \left\lbrace m_{1},\ldots,m_{n-1} \right\rbrace, pri čemu je \left\lbrace m_{1},\ldots,m_{n-2} \right\rbrace ćelija od \pi_{n} , a \left\lbrace m_{2},\ldots,m_{n-1} \right\rbrace njegova vršna figura.
5... u nepoznato
Proučavanje objekata u četvrtoj dimenziji ponajviše se temelji na intuiciji i na dimenzionalnoj analogiji. Ovim malim osvrtom pokušat ćemo razotkriti neke „tajne” ovog prostora.
Napomena 30. U četverodimenzionalnom politopu vršne figure i ćelije su poliedri.
Analogno slučaju n=3 i ovdje ćemo s N_{k} označavati broj k–ćelija politopa.
Teorem 31. Za jednostavno povezane četverodimenzionalne politope vrijedi
N_{0}-N_{1}+N_{2}-N_{3}=0.
Napomena 32. Alternativni dokaz čitatelj može pronaći u [2] , str. 150.
Teorem 33. Postoji 6 regularnih četverodimenzionalnih politopa do na sličnost.
Gore navedeni teorem nećemo dokazivati, budući da je sam dokaz vrlo složen i nije bitan za daljnja razmatranja koja ćemo provesti. Zainteresirani čitatelj dokaz može vidjeti u
| Naziv | Schläflijev simbol | N_{0} | N_{1} | N_{2} | N_{3} |
| \alpha_{4} (5-ćelija) | \left\lbrace 3,3,3 \right\rbrace | 5 | 10 | 10 | 5 |
| \beta_{4} (16-ćelija) | \left\lbrace 3,3,4 \right\rbrace | 8 | 24 | 32 | 16 |
| \gamma_{4} (8-ćelija) | \left\lbrace 4,3,3 \right\rbrace | 16 | 32 | 24 | 8 |
| 24-ćelije | \left\lbrace 3,4,3 \right\rbrace | 24 | 96 | 96 | 24 |
| 120-ćelija | \left\lbrace 3,3,5 \right\rbrace | 600 | 1200 | 720 | 120 |
| 600-ćelija | \left\lbrace 5,3,3 \right\rbrace | 120 | 720 | 1200 | 600 |
Pomnije ćemo proučiti konstrukciju \alpha_{4}, \beta_{4} i \gamma_{4} zato što su njihove generalizacije jedini regularni politopi u većim dimenzijama.
| (1) |
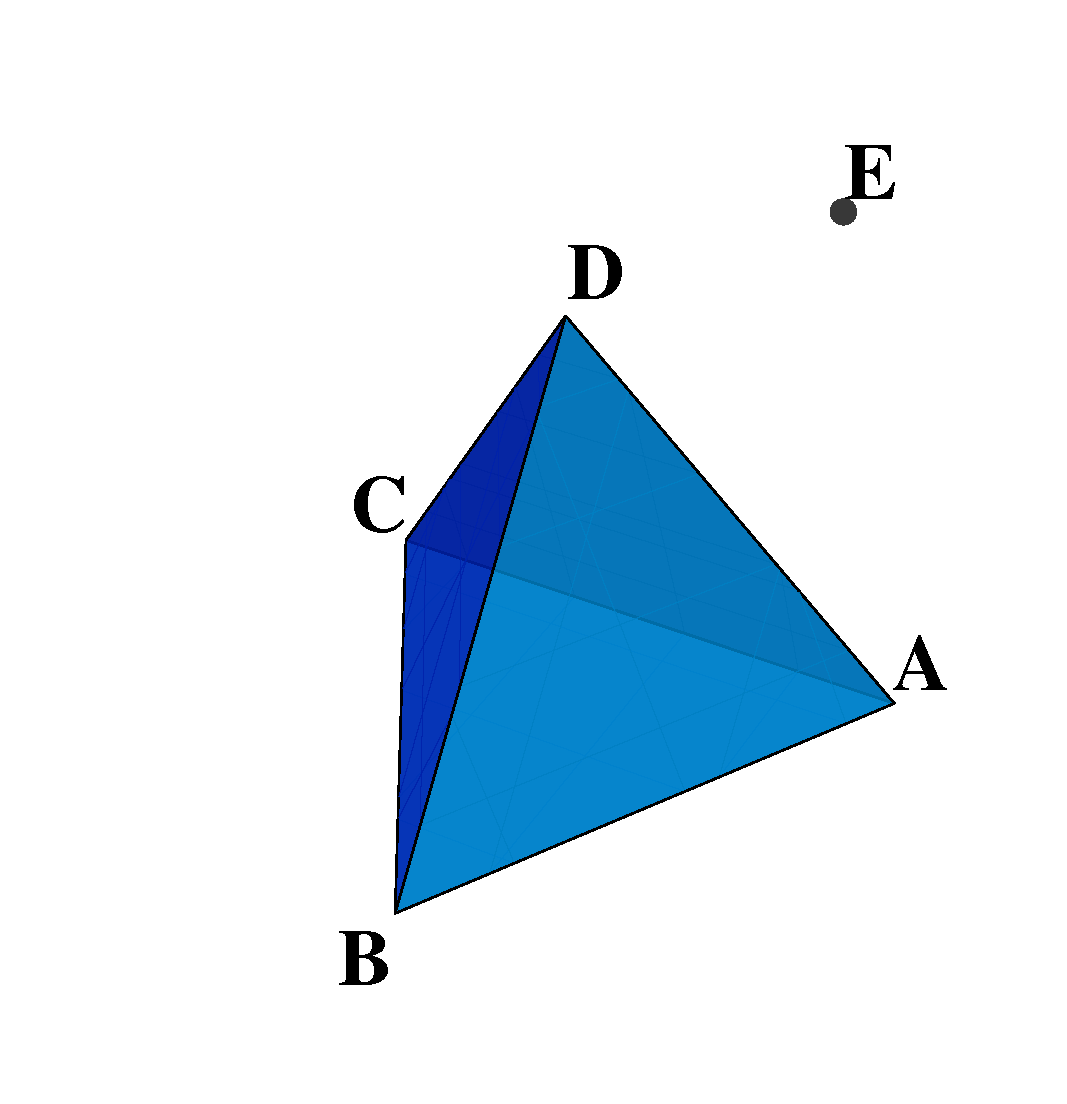
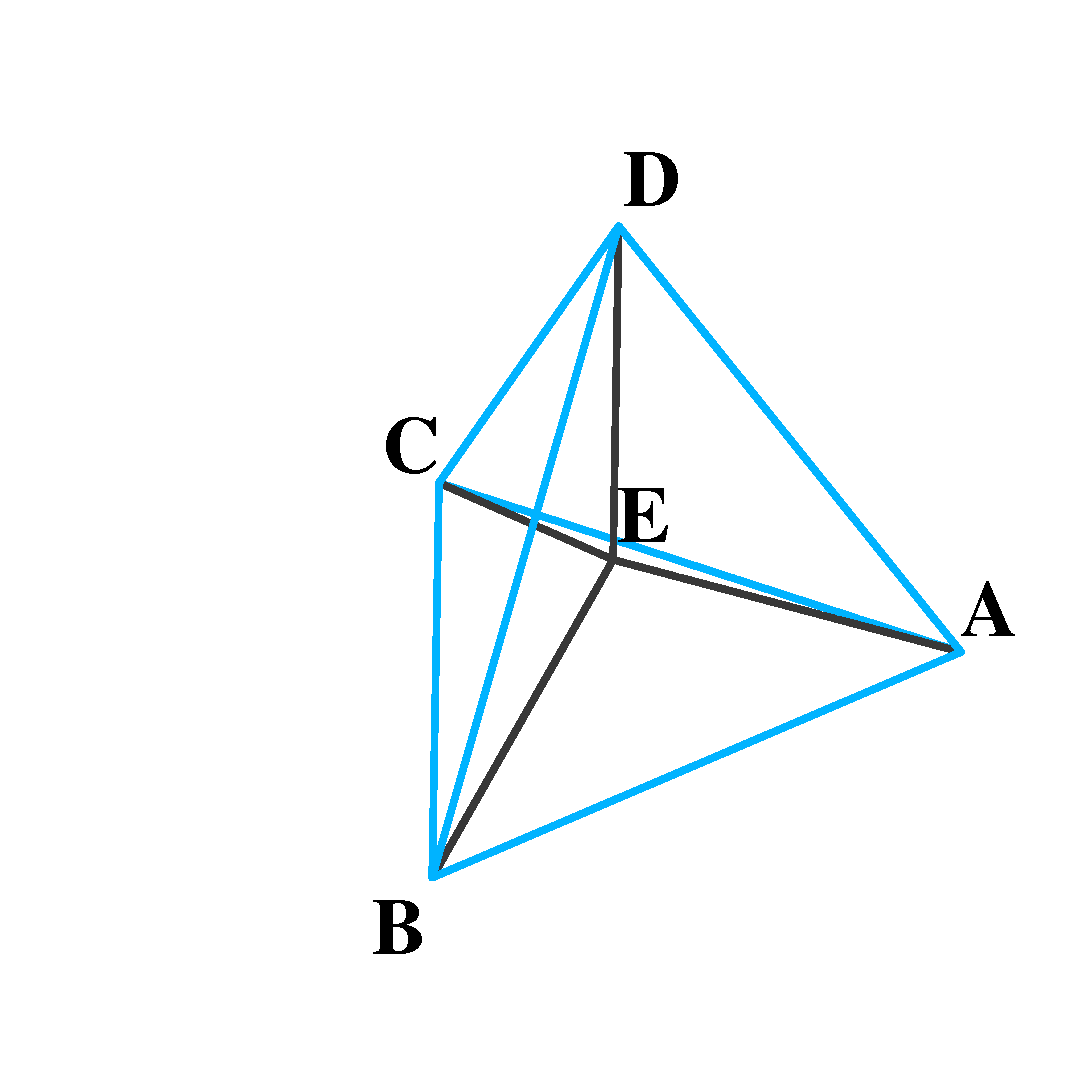
Konstrukciju provodimo u tri koraka. Neka je dana dužina u ravnini - po definiciji je to \alpha_{1}. U sljedećem koraku odabiremo točku tako da ona uz \alpha_{1} čini jednakostraničan trokut. Na taj smo način dobili \alpha_{2}. Nadalje, \alpha_{3} dobivamo odabirom točke u prostoru tako da je ona vrh tetraedra s bazom \alpha_{2}. Sada je jasno da, u četvrtoj dimenziji, uz prikladan odabir točke, dobivamo \alpha_{4}. Navedena konstrukcija prikazana je na slici
\begin{align*} N_{0} &= \left\lbrace A,B,C,D,E \right\rbrace , \\ N_{1} &= \left\lbrace AB, BC, CA, DA, DB, DC, EA, EB, EC, ED \right\rbrace \\ N_{2} &= \left\lbrace ABC, ABD, BCD, ACD, EAB, EBC, ECA, EDA, EDB, EDC \right\rbrace , \\ N_{3} &= \left\lbrace ABCD, EABC, EABD, EBCD, EACD \right\rbrace . \end{align*}
Na slici |
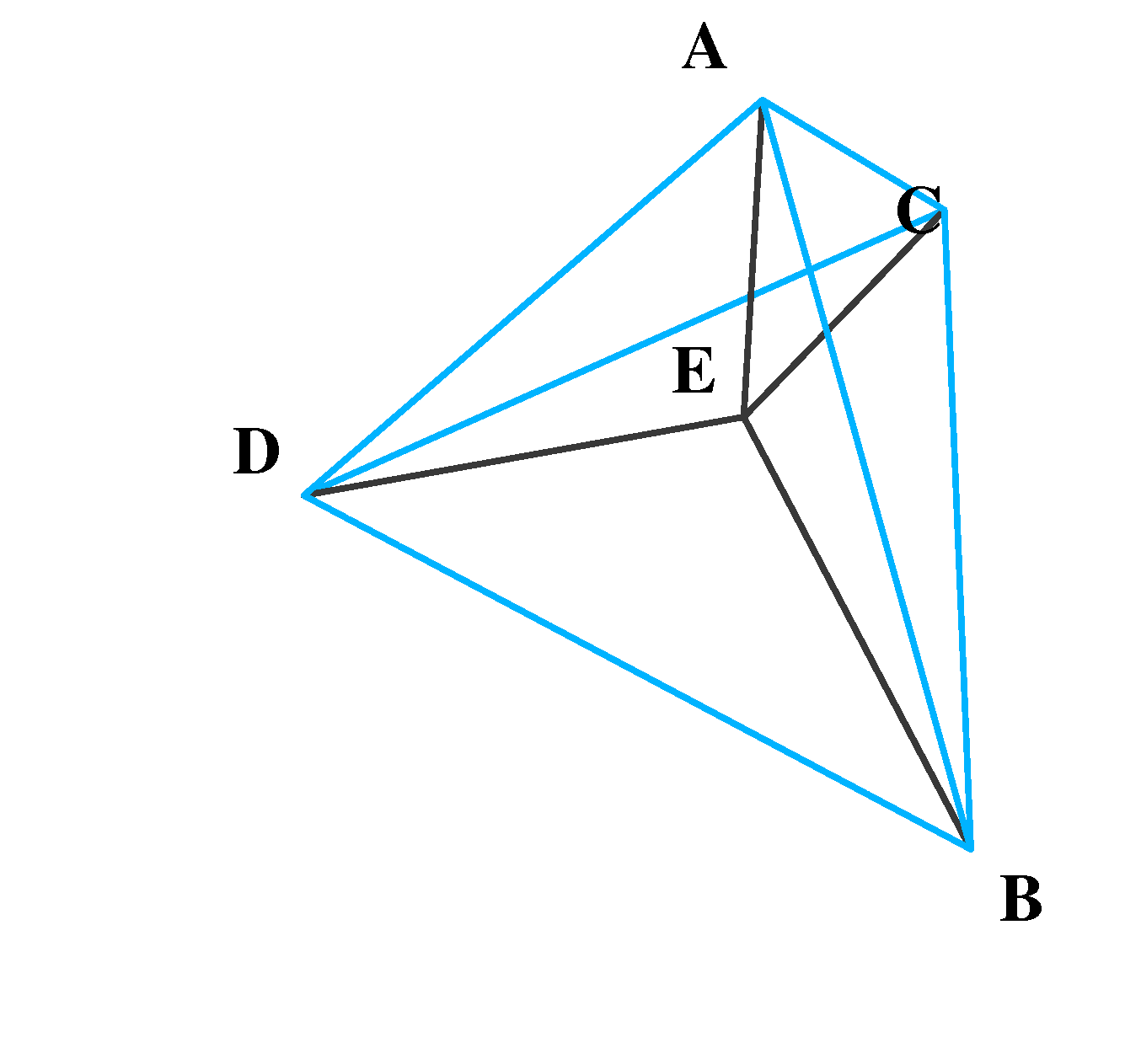
| (2) | Svaki od koraka konstrukcije \beta_{4} sastoji se od odabira odgovarajućih dviju točaka. Konstrukciju započinjemo tako da uzmemo dvije proizvoljne točke u ravnini. Dana dužina je \beta_{1}. Da bismo dobili \beta_{2} , potrebno je izabrati točke takve da je \beta_{1} dijagonala kvadrata kojem su dva vrha odabrane točke. \beta_{2} leži u ravnini koja dijeli prostor na dva dijela. Iz svakog od tih dijelova odabiremo točku takvu da je ona vrh pravilne četverostrane piramide čija je baza \beta_{2}. Jasno je da smo ovime dobili oktaedar – \beta_{3}. \beta_{4} jest generalizacija oktaedra (kao što je \alpha_{4} generalizacija tetraedra) te se dobiva analognim postupkom, samo u višoj dimenziji. Dakle, \beta_{3} leži u prostoru E^{3}\lt E^{4} te dijeli E^{4} na 2 dijela iz kojih odabiremo po jednu točku. Svaka ćelija oktaedra zajedno s novoodabranom točkom čini tetraedar – ćeliju politopa \beta_{4} pa \beta_{4} ima 2\cdot 8=16 ćelija. |
| (3) |
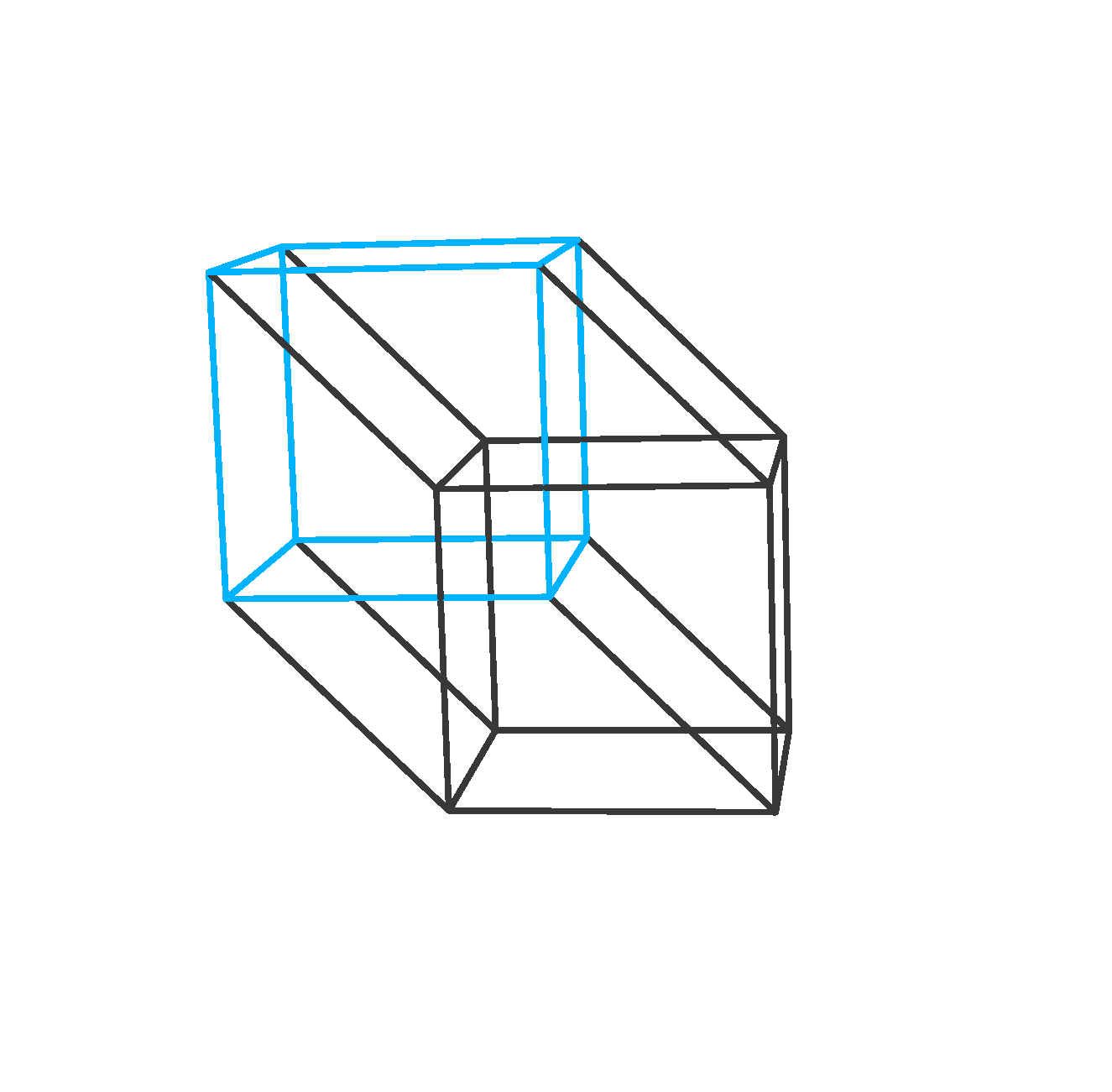
Sljedeća na redu je konstrukcija \gamma_{4}. Pokazat ćemo kako iz točke nizom elementarnih transformacija, preko dužine i kvadrata, dolazimo do kocke. Danu točku ( \gamma_{0} ) „razvučemo” duž proizvoljnog pravca. Dobivenu dužinu ( \gamma_{1} ) „razvučemo” po drugoj dimenziji ne bismo li dobili kvadrat ( \gamma_{2} ) koji potom „razvučemo” po trećoj dimenziji. Na taj način dolazimo do kocke ( \gamma_{3} ), što možete vidjeti na slici |
| 4. | Krenimo redom: 24–ćelije je okrnjen \beta_{4}. Naime, \beta_{4} ima šesnaest 3–ćelija. Iz Schläflijeva simbola vidimo da je riječ o tetraedrima. Kako smo prije pokazali, okrnjeni tetraedar je oktaedar, baš kao i vršna figura politopa \beta_{4}. Budući da \beta_{4} ima 8 vrhova, ima 8 vršnih figura – ponovno je riječ o oktaedrima. Dakle, imamo 24 regularna poliedra. To su upravo 3–ćelije politopa koji konstruiramo. No, da bismo pokazali da je ovako dobiven politop regularan, preostaje pokazati regularnost vršnih figura. Strane vršnih figura 24–ćelije su vršne figure oktaedara pa je jasno da su to kvadrati. Svaki vrh vršne figure zajednički je za tri kvadrata (svaki brid 24– ćelije zajednički je za tri ćelije) pa je polovište zajedničko za tri strane. Zaključujemo da su vršne figure kocke. |
| 5. | Konstrukciju 600–ćelija provodimo preko 24–ćelija. Okrnjen 24–ćelije nije regularan, no „malim trikom” možemo doći do regularnog politopa. Naime, okrnjen politop nekog politopa je konveksan zatvarač skupa polovišta bridova početnog politopa. U našem je slučaju korisno stranice podijeliti u omjeru \left( \sqrt{5}+1 \right) /2. Na taj način okrnjeni oktaedri postaju ikozaedri. Kvadrati, kao vršne figure oktaedra, više ne leže u istoj ravnini, te ih možemo promatrati kao dva trokuta. Analitički se, poznavajući koordinate oktaedra, lako pokazuje da upravo omjer zlatnog reza osigurava regularnost tako dobivenog poliedra. Konveksan zatvarač skupa tako dobivenih točaka je neregularan politop koji se u literaturi označava sa s \left\lbrace 3,4,3 \right\rbrace. Trodimenzionalne ćelije tog politopa čini 120 tetraedara i 24 ikozaedra. Na svakom ikozaedru preostaje konstruirati četverodimenzionalnu piramidu čija je baza upravo dani ikozaedar, a strane 20 regularnih tetraedara. Dobivamo 120+24\cdot 20=600 tetraedara – trodimenzionalne ćelije politopa koji konstruiramo. |
| 6. | 120–ćelija je dualan 600–ćelija. |
6Veće dimenzije
Predmet proučavanja ovog poglavlja su n–dimenzionalni politopi za n\geq 5.
Slijedi već spomenuta Euler–Poincaréova formula:
Teorem 34. Za jednostavno povezan n–dimenzionalni politop \pi_{n} vrijedi
N_{n-1}-N_{n-2}+\ldots+ \left( -1 \right) ^{n-1}N_{0}+ \left( -1 \right) ^{n}=1.
Dokaz. Dokaz provodimo matematičkom indukcijom. Označimo s
Kao i kod Eulerova teorema, promatramo konstrukciju politopa \pi_{n} koji dobivamo spajanjem niza \left( n-1 \right)–dimenzionalnih politopa.
U prvom koraku konstrukcije imamo jedan \pi_{n-1} , stoga je N_{n-1}=1 (upravo on sam), a
Dodajemo sljedeći \pi_{n-1} takav da ima neprazan ( \left( n-2 \right)–dimenzionalni) presjek s dosadašnjom konstrukcijom. Neka taj presjek čini N'_{k}\ k–dimenzionalnih ćelija, k=0,1,\ldots,n-3. Vrijedi
Doprinos zadnje dodanog politopa \pi_{n-1} u sumi
\phi_{n}:=N_{n-1}-N_{n-2}+\ldots+ \left( -1 \right) ^{n-1}N_{0}+ \left( -1 \right) ^{n}.
Za n=2 tvrdnja očito vrijedi (broj vrhova i bridova je jednak), a za n=3 ekvivalentna je Eulerovu teoremu. Pretpostavimo da tvrdnja vrijedi za svaki politop dimenzije d\leq n-1.Kao i kod Eulerova teorema, promatramo konstrukciju politopa \pi_{n} koji dobivamo spajanjem niza \left( n-1 \right)–dimenzionalnih politopa.
U prvom koraku konstrukcije imamo jedan \pi_{n-1} , stoga je N_{n-1}=1 (upravo on sam), a
N_{n-2}-N_{n-3}+\ldots+ \left( -1 \right) ^{n-2}N_{0}+ \left( -1 \right) ^{n-1}=1
vrijedi po pretpostavci indukcije pa je \phi_{n}=0.Dodajemo sljedeći \pi_{n-1} takav da ima neprazan ( \left( n-2 \right)–dimenzionalni) presjek s dosadašnjom konstrukcijom. Neka taj presjek čini N'_{k}\ k–dimenzionalnih ćelija, k=0,1,\ldots,n-3. Vrijedi
N'_{n-3}-N'_{n-4}+\ldots+ \left( -1 \right) ^{n-3}N'_{0}=1- \left( -1 \right) ^{n-2}=:\phi'_{n-2}.
Za dodani politop vrijedi
N''_{n-2}-N''_{n-3}+\ldots+ \left( -1 \right) ^{n-2}N''_{0}=1- \left( -1 \right) ^{n-1}=:\phi''_{n-1}.
Dakle, doprinos dodanog politopa u sumi N_{n-1}-\phi_{n} iznosi \phi''_{n-1}+\phi'_{n-2}-1=1 zbog čega su suma
N_{n-2}-N_{n-3}+\ldots+ \left( -1 \right) ^{n-2}N_{0}
i N_{n-1} uvećani za 1. Stoga je jasno da je \phi_{n}=0.Doprinos zadnje dodanog politopa \pi_{n-1} u sumi
N_{n-2}-N_{n-3}+\ldots+ \left( -1 \right) ^{n-2}N_{0}
je očito 0, dok je za N_{n-1} jednak 1. Time je dokaz teorema završen.
\ \blacksquare
Višedimezionalni prostori siromašniji su regularnim politopima, što možemo uočiti iz sljedećeg teorema.
Teorem 35. Postoje 3 regularna n–dimenzionalna ( n\geq 5 ) politopa do na sličnost.
Politopi o kojima govori prethodni teorem su regularan n–simpleks ( \alpha_{n} ), n–dimenzionalni oktaedar ( \beta_{n} ) i n–dimenzionalna kocka ( \gamma_{n} ) koji su, kao što se da uočiti iz njihovih naziva, generalizacije tetraedra, oktaedra i kocke respektivno te su njihove konstrukcije analogne opisanima u prethodnom poglavlju. Promatrajmo regularan n–simpleks. Iz konstrukcije se vidi da je broj vrhova
N_{0}=n+1 , a budući da svaka dva vrha čine jedan brid, broj bridova je N_{1}=\binom{n+1}{2}. Broj strana je N_{2}=\binom{n+1}{3}\ - svaka tri vrha čine jednu stranu. Vidimo da općenito vrijedi da je broj k–ćelija
N_{k}=\binom{n+1}{k+1},\;\; k=0,1,\ldots,n
Primijetimo da zaista vrijedi teorem
\begin{align*} \phi_{n} &= N_{n-1}-N_{n-2}+\ldots+ \left( -1 \right) ^{n-1}N_{0}+ \left( -1 \right) ^{n} \\ &= \binom{n+1}{n}-\binom{n+1}{n-1}+\ldots+ \left( -1 \right) ^{n-1}\binom{n+1}{1}+ \left( -1 \right) ^{n} \\ &= \binom{n+1}{n+1}- \left[ \binom{n+1}{n+1}-\binom{n+1}{n}+\ldots+ \left( -1 \right) ^{n}\binom{n+1}{1}+ \left( -1 \right) ^{n+1}\binom{n+1}{0} \right] \\ &= 1- \left( 1-1 \right) ^{n+1} \\ &= 1. \end{align*}
Na red dolazi \beta_{n}. Označimo li s N_{k} broj k–ćelija od \beta_{n} i s N'_{k} broj k–ćelija od \beta_{n-1} – iz kojeg konstruiramo \beta_{n} , vrijedi:
\begin{align*} N_{0} & \stackrel{ \left( 1 \right) }{=} N'_{0}+2 \\ N_{1} & \stackrel{ \left( 2 \right) }{=} N'_{1}+2N'_{0} \\ N_{2} & \stackrel{ \left( 3 \right) }{=} N'_{2}+2N'_{1} \\ &\ \vdots \\ N_{k-1} & \stackrel{ \left( k \right) }{=} N'_{k-1}+2N'_{k-2} \\ &\ \vdots \\ N_{n-1} & = N'_{n-1}+2N'_{n-2}. \end{align*}
Pri čemu:
| (1) | dobivamo tako da dodajemo dvije točke, |
| (2) | očito vrijedi, naime, broj već postojećih bridova uvećavamo brojem novonastalih koje dobivamo tako da dodane točke spojimo sa svim vrhovima politopa \beta_{n-1}. Isto tako za |
| (3) | broj 2–ćelija povećan je za dvostruki broj bridova zato što svaki brid u \beta_{n-1} čini 2–ćeliju s jednom od dodanih točaka. Jasno za |
| (4) | zaključujemo analogno. |
N_{k}=2^{k+1}\binom{n}{k+1}, \;\; k=0,\ldots,n-1.
Za bazu uzmimo n=1, k=0. Budući da dužina ima dvije krajnje točke, vrijedi N_{0}=2 , što je u skladu s tvrdnjom. Pretpostavimo da relacija vrijedi u \left( n-1 \right)–voj dimenziji. Neka je k\in \left\lbrace 0,1,\ldots,n-1 \right\rbrace proizvoljan. Tada je:
\begin{align*} N_{k} &= N'_{k}+2N'_{k-1} \\ &= 2^{k+1}\binom{n-1}{k+1}+2\cdot 2^{k}\binom{n-1}{k} \\ &= 2^{k+1} \left[ \binom{n-1}{k+1}+\binom{n-1}{k} \right] \\ &= 2^{k+1}\binom{n}{k+1}. \end{align*}
Pokažimo da za \beta_{n} vrijedi generalizacija Eulerove formule:
\begin{align*} \phi_{n} &= N_{n-1}-N_{n-2}+\ldots+ \left( -1 \right) ^{n-1}N_{0}+ \left( -1 \right) ^{n} \\ &= 2^{n}\binom{n}{n}-2^{n-1}\binom{n}{n-1}+\ldots+ \left( -1 \right) ^{n-1}2^{1}\binom{n}{1}+ \left( -1 \right) ^{n} \\ &= \left( 2-1 \right) ^{n} \\ &= 1. \end{align*}
Za kraj promotrimo poopćenje kocke. Iz konstrukcije je očito da o \gamma_{n} možemo razmišljati kao o „prizmi” čije su baze dva sukladna \gamma_{n-1}. Označimo s N_{k} broj k–ćelija u \displaystyle\gamma_{n} i s N'_{k} broj k–ćelija u \gamma_{n-1}. Vrhove od \gamma_{n} čine vrhovi dviju baza, stoga je N_{0}=2N'_{0}. Bridovi od \gamma_{n} su bridovi dviju baza i bridovi koji spajaju odgovarajuće vrhove baza pa vrijedi jednakost N_{1}=2N'_{1}+N'_{0}. Općenito, k–ćeliju od \gamma_{n} čine ćelije dviju baza i k–ćelije koje nastaju spajanjem odgovarajućih \left( k-1 \right)–ćelija baza. Stoga vrijedi
N_{k}=2N'_{k}+N'_{k-1}, \;\; k=2,\ldots,n-1.
Indukcijom se lako pokaže da je onda
N_{k}=2^{n-k}\binom{n}{k}, \;\; 0\leq k\lt n.
Tvrdnja teorema
\begin{align*} \phi_{n}- \left( -1 \right) ^{n} &= \left( -1 \right) ^{n-1} \left[ \left( 2-1 \right) ^{n}- \left( -1 \right) ^{n} \right] \\ \phi_{n} &= \left( -1 \right) ^{n}+ \left( -1 \right) ^{n-1}+1 \\ \phi_{n} &= 1. \end{align*}
Tabelirajmo dosadašnje rezultate:
| Naziv | Schläflijev simbol | N_{0} | N_{k} | N_{n-1} |
| \alpha_{n} | \left\lbrace 3^{n-1} \right\rbrace | n+1 | \binom{n+1}{k+1} | n+1 |
| \beta_{n} | \left\lbrace 3^{n-2},4 \right\rbrace | 2n | 2^{k+1}\binom{n}{k+1} | 2^{n} |
| \gamma_{n} | \left\lbrace 4,3^{n-2} \right\rbrace | 2^{n} | 2^{n-k}\binom{n}{k} | 2n |
Bibliografija
| [1] | Coxeter, H. S. M.: Regular polytopes, Methuen & Co Ltd., London, 1948 |
| [2] | Sommerville, D. M. Y.: An introduction to the geometry of n dimensions, Dover Publications, Inc, New York, 1958 |
| [3] | Favro, P.; Zucco, A.: Appunti di Geometria Convessa, skripta, Università di Torino |
| [4] | Zucco, A.: Poligoni, poliedri e politopi regolari, Matematicamente.it, 123 (2009), 17.–24. |