Petra Lipovača, Doris Jurišić, Anja Kocijan

Matematičari su od davnina pokazivali osobito zanimanje za izrađivanje geometrijskih konstrukcija s ravnalom i šestarom. Nemogućnost podjele glavnih kutova na tri jednaka dijela s pomoću tih pomagala skrenula je pozornost na podjelu bilo kojeg kuta. Upravo to je bio razlog kasnog pojavljivanja sljedećeg teorema koji glasi: susjedni parovi trisektrisa kuta trokuta uvijek se sijeku na vrhovima jednakostraničnog trokuta. Ovaj teorem otkrio je tek 1904. angloamerički matematičar Frank Morley.

Životopis

Frank Morley rođen je 9. rujna 1860. godine u Velikoj Britaniji u obitelji protestanata. Pohađao je gimnaziju u Woodbridgeu, diplomirao 1884. na Cambridgeu. Bio je jedan od vodećih matematičara. Bavio se najviše algebrom i geometrijom. Osim što je bio izvanredan matematičar, bio je i odličan šahist, te je pobijedio Emanuela Laskera koji je u to vrijeme bio šahovski prvak. Nakon što je diplomirao, Morley je podučavao matematiku. Od 1889. živio je u SAD-u gdje se i oženio. Imao je tri sina među kojima se najviše isticao Frank koji je surađivao s ocem, te su zajedno izdali tri knjige. Zajedno su napisali "Raspravu o teoriji funkcija" 1919., "Uvod u teoriju analitičke funkcije" 1898. i "Inverznu geometriju" 1933. Od 1919. do 1920. Morley je bio predsjednik Američkog matematičkog društva.

Problem trisekcije kuta

Problem trisekcije kuta (dijeljenja kuta na tri jednaka djela):

Za dani kut \(\phi\) mjernog broja (veličine) \(\phi\) treba konstruirati kut mjernog broja \(\frac{\phi}{3}\)

Dokaz nerješivosti:

 Da se dokaže nerješivost konstrukcije ravnalom i šestarom, dovoljno je da to dokažemo za jedan poseban kut.

 Na temelju Moivreove formule imamo:

\[(\cos\frac{\phi}{3}+ i\sin\frac{\phi}{3})^3 = \cos\phi + i\sin\phi\] \[(\cos^3\frac{\phi}{3}-3\cos\frac{\phi}{3}\sin^2\frac{\phi}{3})+i(3\cos^2\frac{\phi}{3}\sin\frac{\phi}{3}-\sin^3\frac{\phi}{3})=\cos\phi + i\sin\phi\]

Slijedi:  \[\sin\phi=3\cos^2\frac{\phi}{3}\sin\frac{\phi}{3}-\sin^3\frac{\phi}{3}\]

ili \[\sin\phi=3\sin\frac{\phi}{3}-4\sin^3\frac{\phi}{3}.\]

Sada možemo smatrati da je \(\sin\phi\) dana veličina, a \(\sin\frac{\phi}{3}\) tražena veličina.

Uvrstimo li  \(\sin\phi=a\) i \(\sin\frac{\phi}{3}=x\),

dobijamo \(4x^3-3x+a=0\).

Ako uvrstimo da je \(y=2x\), dobijemo \(y^3-3y+2a=0\) 

Sada promotrimo slučaj trisekcije kuta od 30˚

\(\sin{30\circ}=\frac{1}{2}\), iz toga slijedi da je \(a=\frac{1}{2}\), pa jednadžba glasi: \(y^3-3y+1=0\)

Kada bi ova konstrukcija bila rješiva, tada bi gornja jednadžba morala imati jedno iz racionalnih brojeva konstruktibilno rješenje.

Prema teoremu koji kaže da kubna jednadžba \(x^3+a_2x^2+a_1x+a_0=0\) s racionalnim koeficijentima nema ni jedno racionalno rješenje, slijedi da ni jedno njeno rješenje nije konstruktibilno iz racionalnih brojeva", pa bi tada jednadžba \(y^3-3y+1=0\) morala imati barem jedno racionalno rješenje. To bi rješenje prema teoremu:"ako neka kubna jednadžba  \(x^3+a_2x^2+a_1x+a_0=0\) s cjelobrojnim koeficijentima ima racionalno rješenje \(x_1\), tada je taj \(x_1\) cijeli broj i djeljtelj od \(a_0\)" moralo biti djeljitelj od 1.

Budući da mi imamo rješenja -1 i 1, a ona nisu rješenja od \(y^3-3y+1=0\), dolazimo do proturječja, odakle vidimo da ova geometrijska konstrukcija nije rješiva ravnalom i šestarom.

Razmotrimo još slučaj  kuta od 90 ̊

Trisekcija kuta je rješiva, kut možemo podijeliti na tri djela.

U tom slučaju je \(a=1\), pa iz jednadžbe:

\(y^3-3y+2a=0\) slijedi \(y^3-3y+2=0\).

Općenito vrijedi da je \(2a\) svaki kut oblika \(\frac{\pi}{2^n}\) gdje je \(n\) neki pozitivni cijeli broj te da je u tom slučaju trisekcija rješiva.

Osim ovih slučajeva postoje i drugi kutovi za koje je trisekcija izvediva.

Ako uzmemo da je s mjerni broj dužine koju smo dobili bilo kojom konstrukcijom iz jedinične dužine i uvrstimo

\(\sin\phi=a=s^3-3s\), pa je time moguće konstruirati i kut \(\phi\).

Sada je pripadajuća jadnadžba ovakvog oblika:

\(y^3-3y-s^3+3s=0\).

Rješenje te jednadžbe je s, pa je time i trisekcija kuta izvediva.

Zbog problema podjele kuta na tri jednaka dijela, odnosno trisekcije, teorem je otkriven tek 1904.

Trisekcija kuta s pomoću trake papira

Ovdje je riječ o mogućnosti izvedbe neke konstrukcije s pomoću ravnala i šestara, a pretpostavimo li uporabu još drugih pomagala, takve se konstrukcije eventualno mogu riješiti.

Sljedeća slika prikazuje vrlo jednostavno i s teorijskog gledišta vrlo zanimljivo rješenje trisekcije kuta pomoću šestara, ravnala i trake papira.

Dan je kut \(3\phi\). Opišemo oko vrha O tog kuta kružnicu polumjera r koja siječe krakove kuta u točkama E i C, zatim nanesemo na rub trake papira točke A i B tako da je duljina AB jednaka duljini polumjera. Položimo tu traku papira na našu ravninu crteža tako da joj točka A bude na pravcu OE i da joj rub prolazi točkom C. Tu traku sada pomičemo tako da točka A bude na pravcu OE i da joj rub stalno prolazi kroz točku C i to tako dugo dok joj točka B ne padne u točku na kružnici.

Ako dalje kut OAB označimo s \(\phi\), lako vidi da kut OBC iznosi \(2\phi\), a kut EOC iznosi \(3\phi\).

Teorem i dokaz

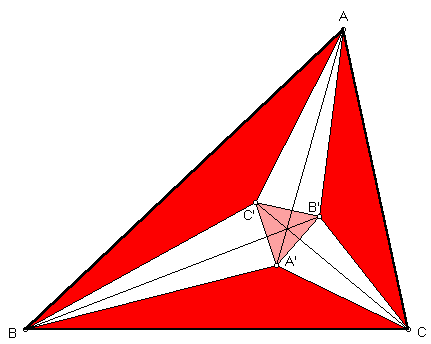
Sjecišta susjednih trisektrisa kutova nekog trokuta su vrhovi jednog jednakostraničnog trokuta.

Prvi dokaz:

Označimo li promatrani trokut s ABC, njegovi su kutovi \(A=3a, B=3b, C=3c\).

Neka se prve dvije susjedne trisektrise nad stranicom BC sijeku u točki P, a druge dvije u točki S. Tada PB i PC raspolavljaju kuteve trokuta SBC. Sa svake strane dužine PS konstruiramo kut od \(30^\circ\) s vrhom u točki P tako da bismo dobili točke Q i R na stranicama SC i SB. Točke P, R, S i Q čine dva trokuta, a to su \(\triangle{PRS}\) i \(\triangle{PQS}\) koji su međusobno sukladni. Iz njihove sukladnosti slijedi da je duljina dužine PR jednaka duljini dužine PQ. Budući da \(\angle{QPR}\) iznosi \(60^\circ\), trokut PQR je jednakostraničan. Ostaje dokazati da su dužine AR i AQ trisektrise \(\angle{BAC}\).

Prenesemo duljinu dužine BP na stranicu BA trokuta BCA s početkom u točki B. Dobivenu točku označimo s M. Sada su \(\triangle{MBR}\) i  \(\triangle{BRP}\) sukladni te je duljina dužine MR jednaka duljini dužine RP. Zatim prenesemo duljinu dužine CP na stranicu CA trokuta BCA i dobijemo točku N, sada su \(\triangle{CNQ}\) i \(\triangle{CPQ}\) sukladni pa je duljina dužine QN jednaka duljini dužine PQ.  Budući da je trokut PQR jednakostraničan, dobivamo da je duljina dužine MR jednaka duljini dužine PQ koja je opet jednaka duljini dužine QN. Zatim smo izračunali mjeru kuta MRQ. Za trokut PRS imali smo na umu da je vanjski kut BRP jednak zbroju unutarnjih kutova S i P.  

Stoga imamo \(\angle{BRP}=\frac{1}{2}S+30^\circ\), a kut BRM je iste veličine pa imamo

\(\angle{MRQ}=360^\circ-2(\frac{1}{2}s+30^\circ)-60^\circ=240^\circ-s\).

Isti argument pokazuje da \(\angle{RQN}\) također iznosi \(240^\circ-S\). Budući da zbroj mjera unutarnjih kutova trokuta iznosi \(180^\circ\), imamo

\(s=180^\circ-(2b+2c)=180^\circ-\frac{2}{3}(3a+3b+3c)+2a=180^\circ-120^\circ+2a=60^\circ+2a\),

stoga

\(\angle{MQR}=\angle{RQN}=240^\circ-(60^\circ+2a)=180^\circ-2a\).

Očita činjenica je da sukladne stranice MR, RQ i QN imaju svoje krajnje točke na kružnici.

Konstrukcijom okomica XO, YO na stranice MR i RQ s početkom u točki O lako je dokazati da su tri trokuta  \(\triangle{OMR}\), \(\triangle{ORQ}\) i \(\triangle{OQN}\) sukladna.

Iz toga slijedi da je duljina dužine ON jednaka duljini dužine OQ, što znači da kružnica sa središtem u O radijusa duljine MO prolazi kroz točke M, R, Q, N. Radijus duljine OR dijeli kut MQR na dva jednaka dijela, a radijus duljine OQ dijeli kut RQN na dva jednaka dijela. Također radijus duljine XO dijeli kut MOR na dva jednaka dijela i radijus duljine YO dijeli kut ROQ na dva jednaka dijela.

Sada imamo

\(\angle{MRO}=\frac{1}{2}\angle{MRQ}=\frac{1}{2}(180^\circ-2a)=90^\circ-a\)

iz čega vidimo da je \(\angle{XOR}=a\), \(\angle{MOR}=2a\), što dovodi do toga da je \(\angle{MON}=6a\).

U ovom krugu tetiva MN sadržava kut od \(6a\) u točki O. U skladu s time, kružni luk MN sadržava kut od \(3a\). No MN sadržava Q u vrhu A dobivenog \(\triangle{ABC}\). Tako krug mora proći kroz točku A. Budući da MR, RQ i QN sadržavaju kut s vrhom u točki O koja je središte kružnice, svi sadržavaju kut, a točka A se također nalazi na toj kružnici. Stoga su AR i AQ trisektrise \(\angle{MAN}\).

Drugi dokaz:

Pođimo obrnutim redoslijedom pa najprije nad stranicama nekog jednakostraničnog trokuta PQR odredimo (prema van) jednakokračne trokute.

Imamo jednakokračne trokute P'QR, Q'RP I R'PQ kojima su kutovi uz baze \(\phi,\rho,\sigma\).

Ti kutovi neka zadovoljavaju uvijete \(\phi<60^\circ, \rho<60^\circ, \sigma<60^\circ\)

\(\phi+\rho+\sigma=120^\circ\)

Sjecišta trisektrisa vrhovi su jednakostraničnog trokuta.

Produžene pobočne stranice tih jednakostraničnih trokuta sijeku se u točkama ABC. Lako se prema slici provjeri da za dani trokut ABC i središte U upisane kružnice vrijedi \(\angle{BUC}=90^\circ+\frac{1}{2}\alpha\).

Primijenimo sada ovo na trokut BCP'.

\(\triangle{BCP}\): Očito imamo najprije

\(\frac{1}{2}\angle{BP'C}=\frac{1}{2}(180^\circ-2\phi)=90^\circ-\phi\)

dok je

\(\angle{BCP}=360^\circ-\phi-(\phi+\rho+\sigma+60^\circ)=180^\circ-\phi=90^\circ+(90^\circ-\phi)\).

Na temelju tog je

\(\angle{BCP}=90^\circ+\frac{1}{2}\angle{BP'C}\).

Ako uz ovo uočimo na osnovi skice da je PP' simetrala kuta \(\angle{BP'C}\), tada vidimo da je točka P središte trokutu BCP' upisane kružnice.

To znači da je PB simetrala od \(\angle{CBP'}\), a PC simetrala od \(\angle{BCP'}\).

Analognim promatranjem trokuta CQ'A i AR'B zaključujemo da je:

QC simetrala od \(\angle{PCA}\),

QA simetrala od \(\angle{CAR}\),

AR simetrala od \(\angle{QAB}\),

BR simetrala od \(\angle{ABP}\).

Prema tome su te simetrale trisektrise kutova trokuta ABC.

Promatranjem trokuta ARQ izlazi odmah:

\(\angle{RAQ}=\frac{1}{3}\alpha=60^\circ-\phi\),

odnosno:

\(\phi=60^\circ-\frac{1}{3}\alpha\)

i analogno tomu:

\(\rho=60^\circ-\frac{1}{3}\beta\)

>te

\(\sigma=60^\circ-\frac{1}{3}\gamma\).

Time nam je omogućeno izračunati kutove \(\phi,\rho,\sigma\) ako je dan trokut ABC (a time i kutovi \(\alpha,\beta,\gamma\)) pa na temelju svih izlaganja možemo iz danog jednakostraničnog trokuta odrediti trokut koji je sličan danom trokutu ABC, čime je ovaj teorem dokazan.

Literatura:

Ross Honsberger. "Mathematical Gems 1"

Dominik Palman: "Geometrijske konstrukcije" Zagreb, 1996.

Dominik Palman: "Trokut i kružnica", Element, Zagreb, 1994.