Ključne riječi: spektar, nelinearni operator, bijekcija


Dobro je poznata važnost spektralne teorije za linearne operatore. Podsjetimo se nekih najznačajnijih osobina spektra linearnih operatora. Neka je X Banachov prostor nad poljem \mathbb{K} realnih ili kompleksnih brojeva.


Za svako \lambda \in \mathbb{K}\setminus \sigma (L) postoji rezolventni operator (\lambda I- L)^{-1} koji je ograničen.


U slučaju da dim X\lt \infty onda je \sigma(L)=\sigma_{p}(L). Primijetimo da \lambda_{0}\in \sigma_{c}(L) povlači da operator (\lambda_{0} I-L) ima inverzni operator (\lambda_{0} I- L)^{-1} ali da taj nije ograničen. Situacija \lambda_{0}\in \sigma_{r}(L) znači da rezolventni operator postoji, ali njegovo područje definicije nije gusto u X; u tom slučaju rezolventni operator može biti ograničen ili neograničen.

Slobodno govoreći, elementi \lambda u subspektru \sigma_{p}(L) karakteriziraju neki gubitak injektivnosti, oni iz \sigma_{r}(L) neki gubitak surjektivnosti, a oni iz \sigma_{c}(L) neki gubitak stabilnosti operatora \lambda I-L.

Ovi dijelovi spektra formiraju disjunktnu podjelu spektra Vrijedi i sljedeći teorem koji daje tzv. formulu spektralnog preslikavanja polinoma.


Spektar linearnog operatora \sigma (L) ima sljedeće važne osobine:

\bullet	zatvoren je i ograničen skup (dakle kompaktan)
\bullet	neprazan je skup kad je \mathbb{K} polje kompleksnih brojeva
\bullet	vrijedi formula spektralnog preslikavanja (2).

Kod definiranja spektra nelinearnih operatora, cilj je, po mogućnosti:

\bullet	u slučaju linearnog operatora da se svodi na poznati spektar (1),
\bullet	da ima bar neke zajedničke osobine s linearnim spektrom (npr. zatvorenost, kompaktnost),
\bullet	da sadrži svojstvene vrijednosti operatora.

S obzirom na definiciju (1) predstavljalo bi izazov definirati spektar neprekidnog linearnog operatora F jednostavno s Ovo ćemo nazivati preslikavajući spektar operatora F. Preciznije mogli bismo proučavati spektar injektivnosti i spektar surjektivnosti pri čemu je \Sigma(F)=\Sigma_{i}(F)\cup \Sigma_{s}(F). Međutim, u nelinearnom slučaju se pokazuje da ovaj pristup nije od neke koristi. Zapravo, ove jednostavne definicje imaju smisla samo u linearnom slučaju, jer tada imamo veoma rigidnu strukturu linearnosti, a također i tako moćno oruđe kao teorem o zatvorenm grafu koji garantira ograničenost inverza ograničenog operatora.

Pokazat ćemo primjerima da preslikavajući spektar (3) ne mora imati ni jednu od poznatih osobina linearnog spektra.

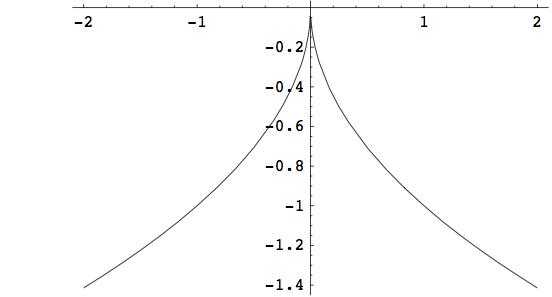
Primjer 2.1 Neka je operator F:\mathbb{R}\rightarrow \mathbb{R} definiran s Odredimo spektre injektivnosti i surjektivnosti, odnosno preslikavajući spektar operatora F. Označimo G(x)=(\lambda I-F)(x)=\lambda x-\sqrt{|x|}.
a) Ispitajmo kad je ovo preslikavanje injektivno.
Za \lambda =0 je G(x)=-\sqrt{|x|}, a to nije injekcija (jer za x\neq 0 vrijedi G(x)=G(-x)). Prema tome, 0 \in \Sigma_{i}(F).

Neka je sada \lambda \neq 0 i promatrajmo jednakosti U slučaju da su x_{1} i x_{2} pozitivni i x_{1}\neq x_{2}, vrijedi Iz uvjeta \frac{1}{\lambda}-\sqrt{x_{1}}\gt 0 dobivamo \lambda \gt 0 i x_{1} \in (0,\frac{1}{\lambda^{2}}).
U slučaju da su x_{1} i x_{2} negativni i x_{1}\neq x_{2}, vrijedi Rješavanjem nejednakosti -\frac{1}{\lambda}-\sqrt{|x_{1}|}\gt 0 dobivamo \lambda \lt 0 i x_{1} \in (-\frac{1}{\lambda^{2}},0). Ovim smo pokazali da za proizvoljno \lambda \gt 0, ako uzmemo x_{1} \in (0,\frac{1}{\lambda^{2}}) i
x_{2}=(\frac{1}{\lambda}-\sqrt{x_{1}})^{2}, onda dobivamo G(x_{1})=G(x_{2}). To znači da za \lambda \in (0,\infty) preslikavanje G nije injektivno, odnosno (0,\infty)\subseteq \Sigma_{i}(F). S druge strane, za proizvoljno \lambda \lt 0, ako uzmemo x_{1} \in (-\frac{1}{\lambda^{2}},0) i x_{2}=-(\frac{1}{\lambda}+\sqrt{|x_{1}|})^{2}, onda opet dobivamo G(x_{1})=G(x_{2}). Dakle, (-\infty,0)\subseteq \Sigma_{i}(F). Sveukupno, našli smo spektar injektivnosti

b) Ispitajmo kad je G surjektivno preslikavanje.
Za \lambda =0 je G(x)=-\sqrt{|x|}, a ovo nije surjekcija jer je G(\mathbb{R})=(-\infty,0]. Prema tome, 0\in \Sigma_{s}(F). Neka je sad \lambda \neq 0 i y \in \mathbb{R} proizvoljno. Ispitajmo rješenja jednadžbe Nalazimo: za \lambda \gt 0 je a za \lambda \lt 0 je Tako da za \lambda \neq 0 i proizvoljno y, postoji x \in \mathbb{R} takav da je G(x)=y; odnosno G je surjekcija. Ostaje samo \Sigma_{s}(F)=\lbrace 0\rbrace . Preslikavajući spektar je pa vidimo da nije ograničen skup.
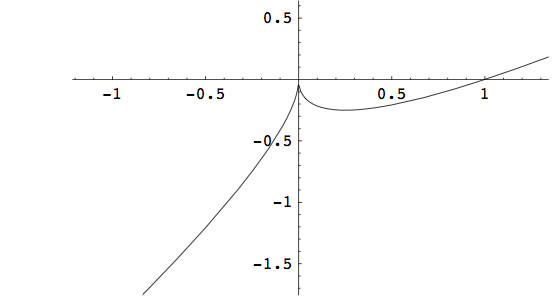
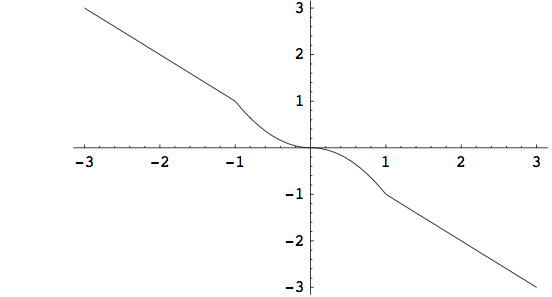
Primjer 2.2 Neka je F:\mathbb{R}\rightarrow \mathbb{R} definiran s U slučaju da je \lambda =0, promatrajmo preslikavanje i pokažimo da je u pitanju bijekcija (vidi sliku 3).

Za y\in (-\infty, -1)\cup (1,\infty),\quad \exists x=-y, tako da G(x)=y. Za y\in [-1,0],\quad \exists x=\sqrt{-y}, tako da G(x)=y. I za y\in [0,1], \exists x=-\sqrt{y},\quad G(x)=y. Dakle, G(\mathbb{R})=\mathbb{R}, pa je G surjekcija i 0\notin \Sigma_{s}(F). Jasno je i da je injekcija jer iz svake jednadžbe G(x_{1})=G(x_{2}) slijedi da je x_{1}=x_{2}. Injektivnost se može dokazati i činjenicom da je G neprekidna i stalno opadajuća funkcija od +\infty do -\infty na čitavoj realnoj osi. Dakle, 0\notin \Sigma_{i}(F). 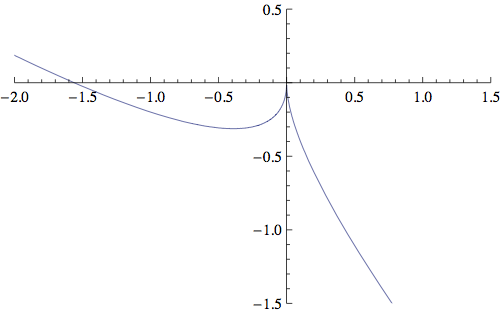Kad je \lambda =1 imamo: G_{max}=G(\frac{1}{2})=\frac{1}{4}, a G_{min}=G(-\frac{1}{2})=-\frac{1}{4} (vidi sliku 4).

Budući da je G neprekidna funkcija, vrijedi G(\mathbb{R})=[-\frac{1}{4}, \frac{1}{4}], pa nije surjekcija i 1\in \Sigma_{s}(F). Jasno je da G nije ni injekcija jer npr. G(2)=G(3)=0. Prema tome, 1\in \Sigma_{i}(F). Neka je \lambda \in (0,1) (vidi sliku 5). Tada

Budući da je G neprekidna funkcija na \mathbb{R} i dostiže lokalni minimum za x=-\frac{\lambda}{2}, a lokalni maksimum za x=\frac{\lambda}{2}, slijedi da nije injekcija. Tako npr. za x_{1}\in (0,\frac{\lambda}{2}) i x_{2}\in (\frac{\lambda}{2}, 1), iz jednadžbe G(x_{1})=G(x_{2}) dobivamo x_{2}=\lambda -x_{1}. Ovim smo pokazali (0,1)\subseteq \Sigma_{i}(F).

Jasno je da je G surjekcija jer je neprekidna funkcija i U slučaju \lambda \in (1,2) je


tako da opet nemamo injekciju, pa (1,2)\subseteq \Sigma_{i}(F). Sada je pa G jest surjekcija. Iz (7) slijedi: za \lambda \geq 2 je G^{\prime}(x)\gt 0, te G stalno raste od -\infty do +\infty; a za \lambda \lt 0 je G^{\prime}(x)\lt 0, pa G stalno opada od +\infty do -\infty na čitavoj realnoj osi. Ovo znači, zbog neprekidnosti, da je za ovakve \lambda preslikavanje G bijekcija. Našli smo, konačno, spektre: Dakle, \Sigma (F) nije zatvoren skup.


Jedna od najvažnijih osobina linearnog spektra je ta da je on uvijek neprazan u slučaju kad je \mathbb{K} polje kompleksnih brojeva. Međutim, pokazuje se da ovo više ne vrijedi kad je riječ o nelinearnom operatoru.

Primjer 2.3 Neka je operator F:\mathbb{C}^{2}\rightarrow \mathbb{C}^{2} definiran s Tada je preslikavanje (\lambda I-F)(z,w)=(\lambda w-i\overline{z}), za svako \lambda \in \mathbb{C}, bijekcija na \mathbb{C}^{2} s inverzom Slijedi da je: Prema tome preslikavajući spektar ovog nelinearnog operatora (9) je prazan skup.
Primjer 2.4 Neka je operator F:\mathbb{R}\rightarrow \mathbb{R} definiran s Nije teško pokazati da je spektar \Sigma (F)=[0,1]. Za polinom p(z)=z^{2} vrijedi p(\Sigma (F))=[0,1]. S druge strane, iz činjenice da je F^{2} (x)\equiv 0 slijedi da je \Sigma (p(F))=\Sigma (F^{2})=\lbrace 0\rbrace. Ovaj primjer pokazuje da ne vrijedi formula spektralnog preslikavanja (2).

Spektar injektivnosti (4) tijesno je povezan s točkovnim spektrom Kao i u linearnom slučaju, elemente \lambda \in \sigma_{p} (F) nazivat ćemo svojstvenim vrijednostima operatora F. U slučaju da je F(0)=0, vrijedi inkluzija koja može biti i stroga. U Primjeru 2.1 imamo da je \sigma_{p} (F)=\mathbb{R}\setminus \lbrace 0\rbrace \subset \mathbb{R}= \Sigma_{i}(F). Naravno, za linearne operatore L uvijek vrijedi da je \sigma_{p} (L)=\sigma_{i} (L), po definiciji.

Pogledajmo sad spektar surjektivnosti (5). Za z\in X definiramo translaciju F_{z} operatora F s Sljedeći rezultat daje nam vezu između spektra surjektivnosti \Sigma_{s}(F) i točkovnog spektra \sigma_{p}(F_{z}) svih translacija (10).




Za F(x)=\sqrt{|x|} iz Primjera 2.1, translatirana funkcija je F_{z}(x)=\sqrt{|x|}+z. Budući da je za svako z\in \mathbb{R} točkovni spektar \sigma_{p}(F_{z})=\mathbb{R}\setminus \lbrace 0\rbrace, na osnovi (11) slijedi da je \Sigma_{s}(F)=\lbrace 0\rbrace.

Primjer 2.5 U prostoru neprekidnih funkcija C[0,1] dan je Hammersteinov integralni operator Operator H je kompozicija H=KF, nelinearnog operatora F definiranog s i linearnog Fredholmova integralnog operatora Odredimo točkovni spektar \sigma_{p}(H). Operator H je kompaktan. Za neprekidnu funkciju x_{n}(t)\equiv n\pi\equiv 0, pa H(x_{n})=0=0x_{n}. To znači da 0 \in \sigma_{p}(H). Razmotrimo sad jednadžbu H(x)=\lambda x, za \lambda \neq 0. Imamo Vrijedi i obrnuto, svaka funkcija x(t)=ct^{\beta +1}, c \neq 0 je svojstvena funkcija operatora H koja odgovara svojstvenoj vrijednosti \lambda =\psi(c). Prema tome, Uvedimo u (12) zamjenu varijabli ct^{\beta +1}=\taudt=\frac{1}{\beta +1} c^{-\frac{1}{\beta +1}} \tau ^{-\frac{\beta}{\beta +1}}d\tau, pa dobivamo Sada je Možemo dodefinirati funkciju \psi u točki 0 tako da bude neprekidna na \mathbb{R}: Budući da je funkcija \widetilde{\psi} neprekidna, vrijedi pri čemu se dostižu sve vrijednosti između lijeve i desne granice. Lijeva strana nejednakosti dostiže se u točkama c=2k \pi, k \in \mathbb{Z}, tj. \psi(2k\pi)= 0. Desna strana nejednakosti ne dobiva se ni za jedno c\neq 0, jer iz \psi (c)=\frac{1}{2(\beta +1)} slijedi Prema tome \sigma_{p} (H)=\Big [0,\frac{1}{2(\beta +1)}\Big ).


Ovim primjerima pokazali smo da nam treba drugačiji pristup pri definiranju spektra nelinearnih operatora. Za nelinearni neprekidni operator F i neku klasu neprekidnih operatora \mathcal{M}(X) koja sadržava F možemo definirati rezolventni skup i spektar Ovisno o tome što uzmemo za klasu \mathcal{M}(X) (npr. neprekidno diferencijabilni, Lipschitz neprekidni, stabilno rješivi ili epi operatori) dobivamo razne spektre. Nazive su dobivali po matematičarima koji su ih prvi uveli: Rhodius, Neuberger, Kachurovski, Feng, itd. Na ovaj način dobivaju se spektri koji imaju samo neke dobre osobine koje imaju spektri linearnog operatora. Nelinearne spektralne teorije i dalje su u razvoju, a opseg njihove primjene vrlo je širok.