De Finettijev teorem
1Uvod
Statistički model i slučajni uzorak osnovni su pojmovi matematičke statistike. Za slučaj beskonačne populacije slučajni uzorak se najčešće definira kao niz nezavisnih i jednako distribuiranih slučajnih veličina u odnosu na svaku vjerojatnost iz pretpostavljenog statističkog modela. Budući da je slučajni uzorak model za niz opažanja određene veličine kao funkcije nekog slučajnog eksperimenta, postavlja se pitanje nije li pretpostavka o nezavisnosti i jednakoj distribuiranosti opažanih pokusa prejaka. Ako jest, koja pretpostavka je slabija od te, a da i dalje povlači poželjne rezultate inferencijalne statistike? Pokazuje se da je to pretpostavka izmjenjivosti.
Koncept izmjenjivosti prvi je uveo Bruno De Finetti3 i upravo nam De Finettijev reprezentacijski teorem objašnjava matematičku vezu između nezavisnosti i izmjenjivosti. Pokazuje se da je izmjenjivost ekvivalentuvjetnoj nezavisnosti i jednakoj distribuiranosti, pri ćemu se uvjetuje u odnosu na neki slučajni element. Teorem kaže da je taj element granična vrijednost parcijalnih empirijskih distribucija koja interpretaciju nalazi u bayesovskom pristupu statistici. Dakle, teorem, u nekom smislu, povezuje frekvencionistički i bayesovski pristup.
U ovome radu nećemo dokazivati De Finettijev teorem. Pokušat ćemo na primjeru niza Bernoullijuevih slučajnih varijabli ilustrirati njegov sadržaj i kako se njime povezuju bayesovski i klasični pristup statistici. Dokaz teorema i nešto detaljnija diskusija posljedica De Finettijevog teorem može se naći u diplomskom radu
2Izmjenjivost
Definicija. Za slučajne varijable X_{1},X_{2},\ldots,X_{n} kažemo da su izmjenjive ako svaka permutacija od \left(X_{1},X_{2},\ldots,X_{n}\right) ima istu zajedničku distribuciju kao i bilo koja druga permutacija. Odnosno
Niz (X_{n})_{n=1}^{\infty} slučajnih varijabli je izmjenjiv ako mu je svaki konačan podskup izmjenjiv.
\left(X_{1},X_{2},\ldots,X_{n}\right) \stackrel{\mathcal{D}}{=}\left(X_{\pi(1)},X_{\pi(2)},\ldots,X_{\pi(n)}\right) \;\; \forall \pi \in S(n),
gdje je S(n) skup svih permutacija skupa \left\lbrace 1,2,\ldots,n\right\rbrace.
Niz (X_{n})_{n=1}^{\infty} slučajnih varijabli je izmjenjiv ako mu je svaki konačan podskup izmjenjiv.
Definiciju izmjenjivosti uveli smo da bismo na najslabiji mogući način izrekli pretpostavku o simetričnosti slučajnih varijabli. Time samo želimo reći da nam je poredak slučajnih varijabli nebitan, odnosno da se budući uzorci ponašaju kao prijašnji uzorci, a ne postavljamo nikakve uvjete na nezavisnost ili postojanje limesa relativnih frekvencija.
Iz definicije vidimo da je izmjenjivost općenitiji pojam od nezavisnosti i jednake distribuiranosti. To znači da je svaki niz (X_{n})_{n=1}^{\infty} nezavisnih i jednako distribuiranih slučajnih varijabli izmjenjiv, ali obrat ne vrijedi (vidjeti Primjer 1.1 u
Pokaže se da je i svaki niz (X_{n})_{n=1}^{\infty} uvjetno nezavisnih i jednako distribuiranih slučajnih varijabli izmjenjiv. Upravo je to jedan od dvaju općenitih oblika izmjenjivosti. Jedini drugi oblik izmjenjivosti je uzorkovanje bez ponavljanja, npr. izvlačenje kuglica iz kutije bez ponavljanja, ali on se odnosi samo na slučaj konačnog niza izmjenjivih slučajnih varijabli (vidjeti 3.2.1 u
3De Finettijev teorem
De Finettijev teorem primijenjen na Bernoullijeve slučajne varijable kaže nam da je izmjenjiv niz Bernoullijevih slučanjih varijabli uvjetno niz nezavnisnih i jednako distribuiranih slučajnih varijabli, i to uz danu varijablu koja predstavlja vrijednost vjerojatnosti uspjeha.
De Finettijev teorem za Bernoullijeve slučajne varijable. Niz (X_{n})_{n=1}^{\infty} Bernoullijevih slučajnih varijabli je izmjenjiv ako i samo ako postoji slučajna varijabla \Theta koja poprima vrijednosti u [0,1] takva da su, uvjetno na \Theta=\theta, (X_{n})_{n=1}^{\infty} nezavisne i jednako distribuirane Bernoullijeve slučajne varijable s parametrom \theta. Nadalje, ako je niz izmjenjiv, onda je distribucija od \Theta jedinstvena i \sum_{i=1}^{n}\frac{X_{i}}{n} konvergira g.s. prema \Theta.
Primjer. Neka su (X_{n})_{n=1}^{\infty} Bernoullijeve slučajne varijable. Pretpostavimo da vrijedi
[2] ). Drugim riječima, moramo još pokazati (vidi uvjete suglasnosti Kolmogorova na stranici 281. u [2] ) da za proizvoljan n \in \mathbb{N} i proizvoljnu n-torku (x_{1},\ldots,x_{n}) elemenata iz \left\lbrace 0,1\right\rbrace vrijedi
Budući da je zadani niz (X_{n})_{n=1}^{\infty} Bernoullijevih slučajnih varijabli izmjenjiv, iz De Finettijeva teorema znamo da niz parcijalnih relativnih frekvencija uspjeha \overline{X}_{n}=\frac{1}{n}\sum_{i=1}^{n}X_{i}, n\in\mathbb{N}, konvergira g.s. prema nekoj slučajnoj varijabli \Theta. Iz toga slijedi da \overline{X}_{n} konvergira i po distribuciji prema \Theta. Neka je F_{n}(t)=\mathbb{P}{\overline{X}_{n}\leqslant t} funkcija distribucije od \overline{X}_{n}. Vrijedi da je
Pretpostavimo sad da smo zabilježili k^{*} uspjeha u prvih n^{*} pokusa, a zanima nas vjerojatnost k uspjeha u sljedećih n pokusa. Označimo s A događaj da se u prvih n^{*} pokusa dogodilo k^{*} uspjeha, a s B događaj da se u sljedećih n pokusa dogodilo k uspjeha. Tada vrijedi
Naprimjer, ako uzmemo da su se u prvih 5 pokusa dogodila 2 uspjeha, tada je vjerojatnost k uspjeha u sljedećih n pokusa jednaka
Lako se vidi da su budući ishodi i dalje izmjenjivi uz dane prošle ishode. Zbog toga, na isti način kao što smo dobili da je početna distribucija od \Theta jednaka U(0,1), možemo izračunati i uvjetnu distribuciju od \Theta uz dani ishod prvih n^{*}
pokusa koristeći se relacijom (1) .
\mathbb{P}(k\text{ uspjeha u }n \text{ pokusa})=\frac{1}{n+1}, \text{ za } k=0,1,\ldots,n \text{ i } n=1,2,\ldots
Ovdje se prirodno pojavljuju dva pitanja. Prvo, postoji li takav niz slučajnih varijabli4 i, drugo, je li takav niz slučajnih varijabli izmjenjiv. Da je takav niz Bernoullijevih slučajnih varijabli izmjenjiv slijedi direktno iz definicije izmjenjivosti. Dakle, preostaje opravdati postojanje takvoga niza. U tu svrhu dovoljno je dokazati konzistentnost zadanih vjerojatnosti pa će postojanje niza slijediti primjenom Kolmogorovljeva teorema (npr. Teorem 9.7 u \begin{align*} \mathbb{P}{X_{1}=x_{1},\ldots,X_{n}=x_{n}} = {} & \mathbb{P}{X_{1}=x_{1},\ldots,X_{n}=x_{n},X_{n+1}=0} \\ & +\mathbb{P}{X_{1}=x_{1},\ldots,X_{n}=x_{n},X_{n+1}=1}. \end{align*}
Stavimo k=\sum_{i=1}^{n}x_{i}. Tada je lijeva strana gornje relacije jednaka \frac{1}{(n+1)\binom{n}{k}}, a desna strana je jednaka
\begin{align*} \frac{1}{(n+2)\binom{n+1}{k}}+\frac{1}{(n+2)\binom{n+1}{k+1}} &= \frac{\frac{n-k+1}{n+1}}{(n+2)\binom{n}{k}}+\frac{\frac{k+1}{n+1}}{(n+2)\binom{n}{k}} \\ &=\frac{1}{(n+1)\binom{n}{k}}. \end{align*}
Time smo dokazali konzistenciju, pa znači da smo vjerojatnosti dobro zadali.
Budući da je zadani niz (X_{n})_{n=1}^{\infty} Bernoullijevih slučajnih varijabli izmjenjiv, iz De Finettijeva teorema znamo da niz parcijalnih relativnih frekvencija uspjeha \overline{X}_{n}=\frac{1}{n}\sum_{i=1}^{n}X_{i}, n\in\mathbb{N}, konvergira g.s. prema nekoj slučajnoj varijabli \Theta. Iz toga slijedi da \overline{X}_{n} konvergira i po distribuciji prema \Theta. Neka je F_{n}(t)=\mathbb{P}{\overline{X}_{n}\leqslant t} funkcija distribucije od \overline{X}_{n}. Vrijedi da je
F_{n}(t)=\mathbb{P}{\text{najviše }nt\text{ uspjeha u }n\text{ pokusa}}=\frac{\left\lfloor{nt}\right\rfloor +1}{n+1},
iz čega se vidi da je \lim_{n\to\infty} F_{n}(t)=\lim_{n\to\infty}\frac{\left\lfloor{nt}\right\rfloor +1}{n+1}=t, i to za sve 0\leqslant t \leqslant 1. Dakle, F(t)=t, 0\leqslant t \leqslant 1, je funkcija distribucije od \Theta=\lim_{n\to\infty}\overline{X_{n}}. Zaključujemo da su (opet prema De Finettijevu teoremu) X_{i}, uvjetno uz dano \Theta=\theta, nezavisne i jednako distribuirane Bernoullijeve slučajne varijable s parametrom \theta i da \Theta ima uniformnu distribuciju U(0,1).
Pretpostavimo sad da smo zabilježili k^{*} uspjeha u prvih n^{*} pokusa, a zanima nas vjerojatnost k uspjeha u sljedećih n pokusa. Označimo s A događaj da se u prvih n^{*} pokusa dogodilo k^{*} uspjeha, a s B događaj da se u sljedećih n pokusa dogodilo k uspjeha. Tada vrijedi
(1)
\mathbb{P}{B\vert A}=\frac{\mathbb{P}{B \cap A}}{\mathbb{P}{A}}=\frac{\frac{\binom{n^{*}}{k^{*}}\binom{n}{k}}{\binom{n^{*}+n}{k^{*}+k}}\frac{1}{n^{*}+n+1}}{\frac{1}{n^{*}+1}} = \frac{\binom{n^{*}}{k^{*}}\binom{n}{k}}{\binom{n^{*}+n}{k^{*}+k}}\frac{n^{*}+1}{n^{*}+n+1}.
(2)
\frac{60\binom{n}{k}}{\binom{n+5}{k+2}}\frac{1}{n+6}.
Alternativno, uvjetnu distribuciju od \Theta možemo dobiti koristeći se sljedećim rezultatom.
Teorem. Neka je (X_{n})_{n=1}^{\infty} niz izmjenjivih Bernoullijevih slučajnih varijabli. Neka je \Theta=\lim_{n\to\infty}\sum_{i=1}^{n}\frac{X_{i}}{n}, i neka je \mu_{\Theta} distribucija od \Theta. Uvjetno na zabilježenih k^{*} uspjeha u prvih n^{*} pokusa funkcija distribucije od \Theta je jednaka
F^{*}(t)=\frac{\int_{[0,t]}\theta^{k^{*}}(1-\theta)^{n^{*}-k^{*}}d\mu_{\Theta}(\theta)}{\int\psi^{k^{*}}(1-\psi)^{n^{*}-k^{*}}d\mu_{\Theta}(\psi)}.
Nastavak primjera. Nakon zabilježenih k^{*} uspjeha u prvih n^{*} pokusa, koristeći se prethodnim teoremom (uz \Theta \sim U(0,1)) možemo izračunati uvjetnu distribuciju od \Theta. Naprimjer, za n^{*}=5 i k^{*}=2 je
(2) za n=1 i k=1. Općenito, nakon opažanja k^{*} uspjeha u n^{*} pokusa dobijemo da je uvjetna funkcija distribucije od \Theta jednaka
Ovaj primjer objašnjava nam zašto su opažene frekvencije važne za računanje vjerojatnosti ako pretpostavljamo da su nam podaci izmjenjivi. Ujedno nam ilustrira vezu bayesovskog pristupa procjeni parametra Bernoullijeva modela s frekvencionističkim.
Neka distribucija \mu_{\Theta} ima gustoću f u odnosu na neku mjeru na [0,1]. Tada će uvjetna gustoća od \Theta uz opaženih k^{*} uspjeha u n^{*} pokusa biti oblika
Ova gustoća veća je za vrijednosti od \theta blizu \frac{k^{*}}{n^{*}} nego što je f. Isto tako, što je n^{*} veći, to uvjetna gustoća ima izraženiji šiljak u blizini \frac{k^{*}}{n^{*}}. Na slikama 1 i 2 nalaze se grafovi uvjetnih gustoća od \Theta za razne k^{*}, n^{*} i f koje ilustriraju upravo navedene činjenice. Ovaj argument na neki način opravdava činjenicu da \Theta često procjenjujemo s \frac{k^{*}}{n^{*}}. To je opravdano jedino kad vjerujemo da su podaci izmjenjivi. Ne tvrdimo da postoji “fiksna vrijednost \theta” takva da su ishodi pokusa nezavisne i jednako distribuirne slučajne varijable s parametrom \theta
. Samo pokušavamo procijeniti (ili predvidjeti) limes relativnih frekvencija.
\begin{align*} F^{*}(\theta) &= \frac{\int_{[0,\theta]}\psi^{2}(1-\psi)^{3}d\mu_{\Theta}(\psi)}{\int\phi^{2}(1-\phi)^{3}d\mu_{\Theta}(\phi)} =\frac{\frac{\Gamma(7)}{\Gamma(3)\Gamma(4)}\int_{[0,\theta]}\psi^{2}(1-\psi)^{3}d\psi}{\underbrace{\int_{0}^{1}\frac{\Gamma(7)}{\Gamma(3)\Gamma(4)}\phi^{2}(1-\phi)^{3}d\phi}_{=1 \text{ (funkcija gustoće od } Beta(3,4))}} \\ &=60\int_{[0,\theta]}\psi^{2}(1-\psi)^{3}d\psi, \text{ za }\theta \in \left\langle0,1\right\rangle, \end{align*}
iz čega slijedi da je uvjetna gustoća jednaka
f^{*}(\theta)=(F^{*})'(\theta)=60\theta^{2}(1-\theta)^{3}, \text{ za } \theta \in \left\langle0,1\right\rangle,
u odnosu na Lebesgueovu mjeru. Mod te distribucije je jednak 2/5 što je relativna frekvencija uspjeha u prvih 5 pokusa. Možemo izračunati i očekivanu vjerojatnost uspjeha u šestom pokusu ako nam je poznato da su se u prvih 5 pokusa dogodila 2 uspjeha. Ona iznosi
\mathbb{E}^{*}\left(\Theta\right)=\int\theta60\theta^{2}(1-\theta)^{3}d\theta=60\frac{\Gamma(4)\Gamma(4)}{\Gamma(8)}\underbrace{\int\frac{\Gamma(8)}{\Gamma(4)\Gamma(4)}\theta^{3}(1-\theta)^{3}d\theta}_{=1 \text{ (funkcija gustoće od }Beta(4,4))}=\frac{3}{7},
što je jednako vjerojatnosti iz \begin{align*} F^{*}(\theta) &= \frac{\int_{[0,\theta]}\psi^{k^{*}}(1-\psi)^{n^{*}-k^{*}}d\psi}{\int_{0}^{1}\phi^{k^{*}}(1-\phi)^{n^{*}-k^{*}}d\phi} =\frac{\frac{\Gamma(n^{*}+k^{*}+2)}{\Gamma(k^{*}+1)\Gamma(n^{*}+1)}\int_{[0,\theta]}\psi^{k^{*}}(1-\psi)^{n^{*}-k^{*}}d\psi}{\underbrace{\int_{0}^{1}\frac{\Gamma(n^{*}+k^{*}+2)}{\Gamma(k^{*}+1)\Gamma(n^{*}+1)}\phi^{k^{*}}(1-\phi)^{n^{*}-k^{*}}d\phi}_{=1 \text{ (funkcija gustoće od }Beta(k^{*}+1,n^{*}-k^{*}+1))}} \\ &=\frac{(n^{*}+1)!}{k^{*}!(n^{*}-k^{*})!}\int_{[0,\theta]}\psi^{k^{*}}(1-\psi)^{n^{*}-k^{*}}d\psi, \text{za }\theta \in \left\langle0,1\right\rangle, \end{align*}
a uvjetna gustoća
f^{*}(\theta)=\frac{(n^{*}+1)!}{k^{*}!(n^{*}-k^{*})!}\theta^{k^{*}}(1-\theta)^{n^{*}-k^{*}}, \text{za } \theta \in \left\langle0,1\right\rangle,
što znači da \Theta ima uvjetno Beta(k^{*}+1,n^{*}-k^{*}+1) distribuciju. Uz dane podatke očekivana vjerojatnost uspjeha u sljedećem pokusu jednaka je uvjetnom očekivanju od \Theta, tj. \frac{k^{*}+1}{n^{*}+2} što je približno jednako \frac{k^{*}}{n^{*}} za velike n^{*}. Primijetite da je mod uvjetne distribucije F^{*} od \Theta upravo jednak \frac{k^{*}}{n^{*}}.
Ovaj primjer objašnjava nam zašto su opažene frekvencije važne za računanje vjerojatnosti ako pretpostavljamo da su nam podaci izmjenjivi. Ujedno nam ilustrira vezu bayesovskog pristupa procjeni parametra Bernoullijeva modela s frekvencionističkim.
Neka distribucija \mu_{\Theta} ima gustoću f u odnosu na neku mjeru na [0,1]. Tada će uvjetna gustoća od \Theta uz opaženih k^{*} uspjeha u n^{*} pokusa biti oblika
(3)
\text{neka konstanta} \cdot \theta^{k^{*}}(1-\theta)^{n^{*}-k^{*}}f(\theta).
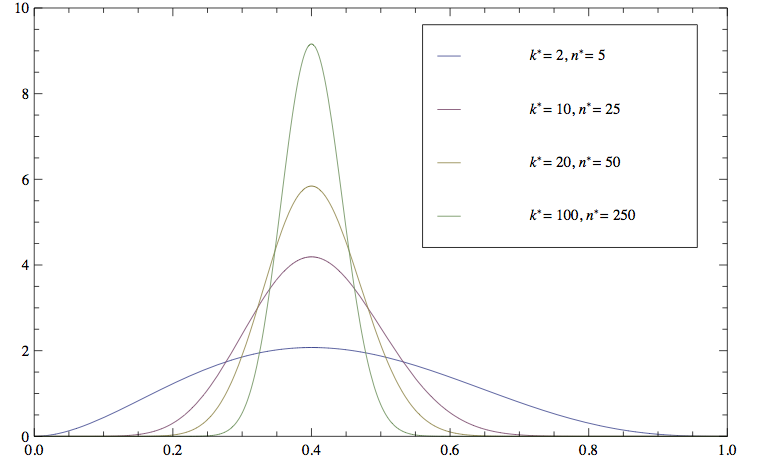
Grafovi funkcija gustoća Beta(k^{*}+1,n^{*}-k^{*}+1)-distribucija za razne k^{*} i n^{*} takve da je k^{*} /n^{*} =2/5=0.4. Te gustoće su ujedno oblika (3 ) za f gustoću uniformne U(0,1)-razdiobe.
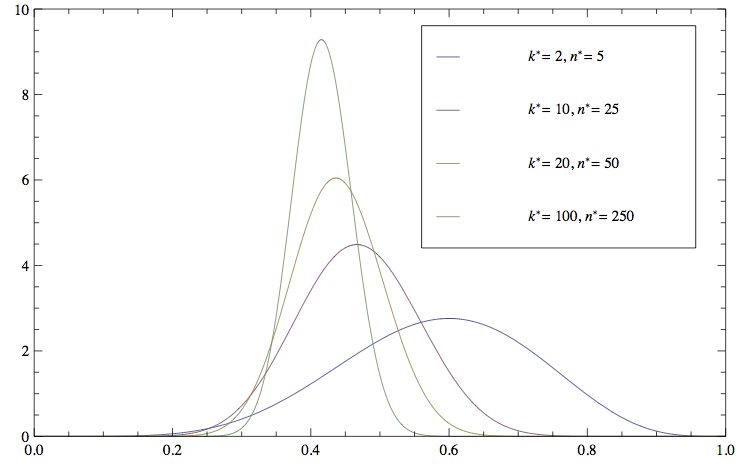
Grafovi funkcija gustoća oblika (3 ) za razne k^{*} i n^{*} takve da je k^{*} /n^{*} =2/5=0.4 i f(\theta )=30\cdot\theta^{4} (1-\theta ).
Zanimljivo je da se De Finettijev teorem može poopćiti i na bilo koji niz izmjenjivih slučajnih varijabli. Znači da je proizvoljan niz slučajnih varijabli izmjenjiv ako i samo ako je to niz nezavisnih i jednako distribuiranih slučajnih varijabli, uvjetno na neku slučajnu veličinu. Štoviše, pokazuje se da ova tvrdnja vrijedi i za posebnu vrstu slučajnih elemenata, koji su poopćenje slučajnih varijabli.
Taj opći De Finettijev reprezentacijski teorem govori nam sljedeće:
De Finettijev teorem. Neka je \left(S,\mathcal{A},\mu\right) vjerojatnosni prostor i (\mathcal{X},\mathcal{B}) Borelov prostor. Neka su X_{n}:S\to\mathcal{X}, n \in \mathbb{N}, izmjerive funkcije. Tada je niz (X_{n})_{n=1}^{\infty} slučajnih elemenata izmjenjiv ako i samo ako postoji slučajna vjerojatnosna mjera \textbf{P} na (\mathcal{X},\mathcal{B}) takva da su, uvjetno na \textbf{P}=P, (X_{n})_{n=1}^{\infty} nezavisni i jednako distribuirani s distribucijom P. Nadalje, ako je niz izmjenjiv, tada je distribucija od \textbf{P} jedinstvena i \textbf{P}_{n}(B) konvergira prema \textbf{P}(B) g.s. za svaki B \in \mathcal{B}
.
Razlika u odnosu na Bernoullijev slučaj je ta što za proizvoljan niz (X_{n})_{n=1}^{\infty} izmjenjivih slučajnih elemenata koji poprimaju vrijednosti u Borelovu prostoru postoji neka slučajna vjerojatnosna mjera \textbf{P}, a ne slučajna varijabla, u odnosu na koju su X_{i} uvjetno nezavisni i jednako distribuirani. Tu slučajnu vjerojatnosnu mjeru \textbf{P} dobijemo kao limes empirijskih distribucija \textbf{P}_{n} od X_{1},\ldots,X_{n}. Podsjetimo se, empirijska distribucija od X_{1},\ldots,X_{n} je slučajna vjerojatnosna mjera definirana izrazom5\textbf{P}_{n} (B):=\frac{1}{n}\sum_{i=1}^{n} \mathbf{1}_{B}(X_{i}) za svaki Borelov skup B.
Jedino nam preostaje vidjeti što je zapravo slučajna vjerojatnosna mjera. U Bernoullijevu slučaju vidimo da je to neka slučajna varijabla s vrijednostima u intervalu [0,1]. Za slučajne elemente koji mogu poprimiti samo konačno mnogo vrijednosti slučajne vjerojatnosne mjere su ekvivalentne slučajnim vektorima. Za proizvoljne slučajne elemente slučajne vjerojatnosne mjere su nešto složenije, ali se također definiraju kao jedna vrsta izmjerivih preslikavanja.
Bibliografija
1Kristina Ana Škreb, mag. math., [email protected]
2Dr. sc. Miljenko Huzak, docent, PMF-Matematički odsjek, Zagreb, [email protected]
3Bruno De Finetti, rođen 13. lipnja 1906. u Innsbrucku, umro 20. srpnja 1985. u Rimu (vidjeti [1] ).
4U smislu da postoji vjerojatnosni prostor i da je na njemu definiran niz slučajnih varijabli sa zadanim svojstvom.
5Funkcija x\mapsto\mathbf{1}_{A}(x) je karakteristična funkcija skupa A. Definira se kao funkcija \mathbf{1}_{A}:\mathbb{R}\mapsto\lbrace 0,1\rbrace takva da je \mathbf{1}_{A}(x)=1 ako i samo ako je x\in A.