Blaženka Bakula,
Magistra edukacije matematike, zaposlena u Srednjoj školi A.B.Šimića, Grude, BiH, [email protected] |
Zrinka Franušić
Docentica na PMF-Matematičkom odsjeku u Zagrebu, [email protected] |
U prostranstvu cjelobrojnih nizova Fibonaccijev niz ne gubi svoj sjaj već više od osam stoljeća, točnije od kad se pojavio u knjizi Liber Abaci talijanskog matematičara Leonarda Bonaccija poznatog i kao Leonardo Pisano, a najpoznatijeg kao Fibonacci. Bez pretjerivanja, riječ je o jednom od najpoznatijih nizova koji privlači i fascinira kako profesionalce tako i potpune amatere. Nadalje, neprestano iznenađuje sa svojom prisutnošću u očekivanim, ali i potpuno neočekivanim situacijama. O Fibonaccijevim brojevima postoji vrlo velika količina informacija, mnoštvo publikacija, knjiga, te internetskih sadržaja. U ovom radu pokazat ćemo i dokazati neke zanimljive identitete vezane uz Fibonaccijeve brojeve koristeći jednostavnu algebru matrica i determinanti. Između ostalog, pokazujemo i poznati Cassinijev identitet koji se se može povezati s problemom popločavanja. Zbog mlađeg čitateljstva navest ćemo osnovna svojstva Fibonaccijevog niza, te osnovne pojmove iz linearne algebre.
1Fibonaccijevi brojevi
Fibonaccijev niz je niz brojeva
1,1,2,3,5,8,13,21,34,55,\ldots.
Niz bi s lakoćom nastavili članom 89 koji je zbroj prethodna dva. Iskažimo njegovu matematičku definiciju.
Definicija 1. Neka je
F_{1}=1 i
F_{2}=1. Niz
(F_{n}) definiran rekurzivnom relacijom
za
n\geq 3 naziva se
Fibonaccijev niz. Član niza
F_{n} zove se
n-ti
Fibonaccijev broj.
Napomenimo da se ponekad za početne vrijednosti niza uzimaju vrijednosti F_{0}=0 i F_{1}=1.
U već spomenutoj knjizi Liber Abaci taj niz predstavlja rješenje problema o razmnožavanju zečeva. Pretpostavimo da 1. siječnja raspolažemo s jednim parom zečeva. Taj par dobiva po jedan par mladih zečeva svakog prvog dana u mjesecu, počevši od 1. ožujka. Svaki novi par dobiva po jedan par zečeva svakog prvog dana u mjesecu, ali tek nakon navršena dva mjeseca života. Problem je koliko će parova zečeva biti nakon n mjeseci. Odgovor je upravo n-ti Fibonaccijev broj F_{n}.
Eksplicitno, Fibonaccijeve brojeve možemo izračunati pomoću formule
F_{n}=\frac{1}{\sqrt{5}}(\alpha^{n}-\beta^{n}),
pri čemu su \alpha i \beta korijeni takozvane zlatne jednadžbe
x^{2}-x-1=0,
to jest
\alpha=\frac{1+\sqrt{5}}{2},\ \beta=\frac{1-\sqrt{5}}{2}.
Konstanta \alpha poznatija je pod nazivom zlatni rez.
Uz Fibonaccijev niz često se veže i Lucasov niz (L_{n}) koji je definiran istom rekurzijom (1).
Definicija 2. Neka je
L_{0}=2 i
L_{1}=1. Niz
(L_{n}) definiran rekurzivnom relacijom
za
n\geq 2 naziva se
Lucasov niz.
Predodžbe radi, prvih nekoliko članova Lucasova niza su
2,1,3, 4, 7, 11, 18, \ldots .
Eksplicitno ih računamo pomoću formule
L_{n}=\alpha^{n}+\beta^{n}.
Fibonaccijevi i Lucasovi brojevi zadovoljavaju različite algebarske identitete. Budući da su generirani rekurzivnim relacijama (1) i (2), prirodno je takve identitete dokazivati pomoću principa matematičke indukcije. Prisjetimo ga se. Ako je neka tvrdnja točna za broj 1 i ako iz pretpostavke da tvrdnja vrijedi za prirodni broj n slijedi da je ispravna i za sljedeći broj n+1, tada ona vrijedi za svaki prirodni broj n.
Kao primjer navodimo osnovnu relaciju koja povezuje Fibonaccijeve i Lucasove brojevi, to jest
za n\geq 1. Jednakost pokazujemo pomoću principa matematičke indukcije. Za n=1 jednakost vrijedi jer je
F_{0}+F_{2}=1=L_{1}.
Pretpostavimo sada da jednakost vrijedi za n=k, odnosno L_{k}=F_{k-1}+F_{k+1}. Za n=k+1 imamo
\begin{align*} F_{k}+F_{k+2}=&F_{k-1}+F_{k-2}+F_{k+1}+F_{k} =(F_{k-1} + F_{k+1} + (F_{k-2} + F_{k}) =L_{k}+L_{k-1} =L_{k+1}, \end{align*}
što je i trebalo pokazati.
U onom što slijedi pokazat ćemo kako možemo dokazati i izvesti još identiteta s Fibonaccijevim i Lucasovim brojevima koristeći elementarna svojstva matrica.
2Matrice i determinante reda 2
Matrica reda 2 je kvadratna shema koja se sastoji od 4 elementa posložena u 2 retka i 2 stupca. Simbolički ju zapisujemo kao
A=\left( \begin{array}{rr} a_{11} &a_{12} \\\ a_{21} &a_{22} \end{array} \right).
Elementi matrice a_{11}, a_{12}, a_{21}, a_{22} su najčešće realni brojevi, pa takvu matricu nazivamo realnom. Elementi matrice su indeksirani tako da nas upućuju na kojoj se poziciji u matrici nalaze. Tako se element a_{21} nalazi na presjeku drugog retka i prvog stupce. Na skupu svih matrica reda 2 jednostavno uvodimo dvije operacije, zbrajanje matrica i množenje matrica skalarom (realnim brojem). Te se operacije izvršavaju prirodno, 'po elementima'. Dakle,
A+B=\left( \begin{array}{rr} a_{11} &a_{12} \\\ a_{21} &a_{22} \end{array} \right)+\left( \begin{array}{rr} b_{11} &b_{12} \\\ b_{21} &b_{22} \end{array} \right)=\left( \begin{array}{rr} a_{11}+b_{11} &a_{12}+b_{12} \\\ a_{21}+b_{21} &a_{22}+b_{22} \end{array} \right),
\alpha\cdot A=\alpha\left( \begin{array}{rr} a_{11} &a_{12} \\\ a_{21} &a_{22} \end{array} \right)=\left( \begin{array}{rr} \alpha a_{11} &\alpha a_{12} \\\ \alpha a_{21} &\alpha a_{22} \end{array} \right).
Na primjer,
\left(\begin{array}{rr} 1 &2 \\\ 3 &4 \end{array} \right)+\left( \begin{array}{rr} -4 &-3 \\\ -2 &-1 \end{array} \right)=\left( \begin{array}{rr} -3 &-1 \\\ 1 &3 \end{array} \right),
3\left( \begin{array}{rr} 1 &2 \\\ -1 &0 \end{array} \right)=\left( \begin{array}{rr} 3 &6 \\\ -3 &0 \end{array} \right).
Množenje matrica ne ćemo definirati po analogiji i to je prilično neočekivano. Umnožak ili produkt dviju matrica definiramo na sljedeći način
A\cdot B=\left( \begin{array}{rr} a_{11} &a_{12} \\\ a_{21} &a_{22} \end{array} \right)\cdot\left( \begin{array}{rr} b_{11} &b_{12} \\\ b_{21} &b_{22} \end{array} \right)= \left(\begin{array}{rr} a_{11}b_{11}+a_{12}b_{21} &a_{11}b_{12}+a_{12}b_{22} \\\ a_{21}b_{11}+a_{22}b_{21} &a_{21}b_{12}+a_{22}b_{22} \end{array}\right).
Na primjer,
\left(\begin{array}{rr} 1 &2 \\\ 3 &4 \end{array} \right)\cdot\left( \begin{array}{rr} -4 &-3 \\\ -2 &-1 \end{array} \right)=\left( \begin{array}{rr} -8 &-5 \\\ -20 &-13 \end{array}\right).
Zbog ovakve 'neobične' definicije i množenje matrica imat će neka 'neobična' svojstva. Na primjer, općenito ne će vrijediti svojstvo komutativnosti.
Uz matricu reda 2 često vežemo i pojam determinante. To je broj koji pridružujemo matrici, a definiramo ga kao
\det A=|A|= a_{11} a_{22}-a_{12}a_{21}.
Zahvaljući 'neobično' definiranom množenju matrica vrijedit će sljedeće važno svojstvo, u matematici poznatije kao Binet-Cauchyjev teorem,
|A\cdot B|=|A|\cdot|B|.
Provjerimo to na gornjem primjeru,
\left|\begin{array}{rr} 1 &2 \\\ 3 &4 \end{array} \right|=-2,\ \left| \begin{array}{rr} -4 &-3 \\\ -2 &-1 \end{array} \right|= -2,\left| \begin{array}{rr} -8 &-5 \\\ -20 &-13 \end{array}\right|=4.
3Identiteti s Fibonaccijevim i Lucasovim brojevima
Matricu Q definirat ćemo kao
Q=\left( \begin{array}{rr} 1 &1 \\\ 1 &0 \end{array} \right).
Primijetimo da je determinanta matrice Q jednaka |Q| =-1. Nadalje, vrijedi
Q^{2}= \left( \begin{array}{rr} 1 &1 \\\ 1 &0 \end{array} \right) \left( \begin{array}{rr} 1 &1 \\\ 1 &0 \end{array} \right) = \left( \begin{array}{rr} 2 &1 \\\ 1 &1 \end{array} \right),
Q^{3}=\left( \begin{array}{rr} 1 &1 \\\ 1 &0 \end{array} \right) \left( \begin{array}{rr} 2 &1 \\\ 1 &1 \end{array} \right)= \left( \begin{array}{rr} 3 &2 \\\ 2 &1 \end{array} \right),
Q^{4}= \left( \begin{array}{rr} 1 &1 \\\ 1 &0 \end{array} \right) \left( \begin{array}{rr} 3 &2 \\\ 2 &1 \end{array} \right)=\left( \begin{array}{rr} 5 &3 \\\ 3 &2 \end{array} \right).
Uočimo da se u matricama Q^{2}, Q^{3}, Q^{4} pojavljuju Fibonaccijevi brojevi. Nije teško pretpostaviti kako će izgledati matrica Q^{n}.
Teorem 3. Neka je
n\geq1. Tada
(4)
Q^{n}=\left( \begin{array}{rr} F_{n+1} &F_{n} \\\ F_{n} &F_{n-1} \end{array} \right).
Dokaz 4. Neka je
n=1.
Q^{1}=\left( \begin{array}{rr} F_{2} &F_{1} \\\ F_{1} &F_{0} \end{array} \right)\left( \begin{array}{rr} 1 &1 \\\ 1 &0 \end{array} \right)=Q.
Pretpostavimo da (
4) vrijedi za
n=k\geq1. Želimo pokazati da (
4) vrijedi za
n=k+1. Zaista,
Q^{k+1}=Q^{k} Q^{1}=\left( \begin{array}{rr} F_{k+1} &F_{k} \\\ F_{k} &F_{k-1} \end{array} \right) \left( \begin{array}{rr} 1 &1 \\\ 1 &0 \end{array} \right)= \left( \begin{array}{rr} F_{k+1}+F_{k} &F_{k+1} \\\ F_{k} + F_{k-1} &F_{k} \end{array} \right) = \left( \begin{array}{rr} F_{k+2} &F_{k+1} \\\ F_{k+1} &F_{k} \end{array} \right).
Prema principu matematičke indukcije slijedi da formula (
4) vrijedi za svaki
n\in\mathbb{N}.
Pomoću Teorema 3 dokazujemo poznatu Cassinijevu formulu za Fibonaccijeve brojeve.
Korolar 5.[Cassinijeva formula] Neka je
n\geq 1. Tada je
(5)
F_{n-1}F_{n+1}-F_{n}^{2}=(-1)^{n}.
Dokaz 6. Budući da je
|Q| =-1, prema Binet-Cauchyjevom teoremu slijedi da je
|Q^{n}| =(-1)^{n}. Iz Teorema
3 slijedi da je
|Q^{n}|=F_{n-1}F_{n+1}-F_{n}^{2}, pa je
F_{n-1}F_{n+1}-F_{n}^{2}=(-1)^{n}.
Kombinatorni dokaz i interpretaciju jednakosti (5) dat ćemo u sljedećem poglavlju. Nadalje, kao posljedicu Teorema 3 imamo i sljedeće četiri jednakosti:
Korolar 7. Vrijedi
(6)
\begin{eqnarray} && F_{m+n+1}=F_{m+1}F_{n+1} +F_{m} F_{n},\\\ && F_{m+n}=F_{m+1} F_{n} + F_{m} F_{n-1},\\\ && F_{m+n}=F_{m} F_{n+1} + F_{m-1}F_{n},\\\ && F_{m+n-1}=F_{m} F_{n}+F_{m-1}F_{n-1} \end{eqnarray}
za sve
m,n\geq1.
Dokaz 8. Budući da je
Q^{m} Q^{n}=Q^{m+n}, imamo
\left( \begin{array}{rr} F_{m+1} &F_{m} \\\ F_{m} &F_{m-1} \end{array} \right) \left( \begin{array}{rr} F_{n+1} &F_{n} \\\ F_{n} &F_{n-1} \end{array} \right) = \left( \begin{array}{rr} F_{m+n+1} &F_{m+n} \\\ F_{m+n} &F_{m+n-1} \end{array} \right).
Množenjem matrica dobivamo
\left( \begin{array}{rr} F_{m+1}F_{n+1}+F_{m}F_{n} &F_{m+1}F_{n}+F_{m}F_{n-1} \\\ F_{m}F_{n+1}+F_{m-1}F_{n} &F_{m}F_{n}+F_{m-1}F_{n-1} \end{array} \right) = \left( \begin{array}{rr} F_{m+n+1} &F_{m+n} \\\ F_{m+n} &F_{m+n-1} \end{array} \right)
odkuda slijede tražene jednakosti.
Neka je m=n. Tada jednakost (6) daje formulu za računanje Fibonaccijevih brojeva s neparnim indeksom
F_{n}^{2} +F_{n+1}^{2} =F_{2n+1},
a jednakost (6) formulu za računanje Fibonaccijevih brojeva s parnim indeksom
F_{2n}=F_{n+1} F_{n} + F_{n} F_{n-1}=F_{n} (F_{n+1}+F_{n-1}),
odnosno
F_{2n}=F_{n}L_{n}.
Korolar 9. Vrijedi
F_{m+1}L_{n}+F_{m}L_{n-1}=L_{m+n}
za
m\geq0,
n\geq1. \end {cor}
Dokaz 10. Zbrajanjem jednakosti (
6) i jednakosti
F_{m+n-1} = F_{m+1}F_{n-1} + F_{m}F_{n-2} koju smo dobili zamjenom
n s
n-1 u (
6), dobivamo
F_{m+1}(F_{n+1} + F_{n-1}) + F_{m}(F_{n} + F_{n-2}) = F_{m+n+1} + F_{m+n-1}.
Primjenom jednakosti (
3) slijedi
F_{m+1}L_{n} + F_{m}L_{n-1} = L_{m+m},
što je i trebalo dokazati.
Evo još jedne jednakosti koji povezuje Fibonaccijeve i Lucasove brojeve.
Korolar 11. Vrijedi
(7)
2F_{m+n}=F_{m}L_{n}+F_{n}L_{m}
za
m,\,n\geq0. \end {cor}
Dokaz 12. Zbrajanjem jednakosti (
6) i (
6) dobivamo
2F_{m+n}=F_{m}(F_{n-1}+ F_{n+1}) + F_{n} ( F_{m+1}+F_{m-1})=F_{m}L_{n}+F_{n}L_{m} .
Teorem 13. Vrijedi
Q^{n}\left( \begin{array}{rr} 1 &2 \\\ 2 &-1 \end{array} \right)=\left( \begin{array}{ll} L_{n+1} &L_{n} \\\ L_{n} &L_{n-1} \end{array} \right).
Dokaz 14.
Q^{n}\left( \begin{array}{rr} 1 &2 \\\ 2 &-1 \end{array} \right)= \left( \begin{array}{ll} F_{n+1} &F_{n} \\\ F_{n} &F_{n-1} \end{array} \right)\left( \begin{array}{rr} 1 &2 \\\ 2 &-1 \end{array} \right)=\left(\begin{array}{rr} F_{n+1}+2F_{n} &2F_{n+1}-F_{n} \\\ F_{n}+2F_{n-1} &2F_{n}-F_{n-1} \end{array} \right).
Primjenom jednakosti (
3) dobivamo traženu jednakost. Na primjer,
F_{n+1}+2F_{n}=F_{n+1}+F_{n}+F_{n}=F_{n+2}+F_{n}=L_{n+1}.
Korolar 15. Vrijedi
(8)
L_{n-1}L_{n+1}-L_{n}^{2}=5(-1)^{n+1}.
Dokaz 16. Prema Teoremu
13 i Binet-Cauchyjevom teoremu slijedi
\left| \begin{array}{rr} F_{n+1} &F_{n} \\\ F_{n} &F_{n-1} \end{array} \right|\left| \begin{array}{rr} 1 &2 \\\ 2 &-1 \end{array} \right|=\left| \begin{array}{rr} L_{n+1} &L_{n} \\\ L_{n} &L_{n-1} \end{array} \right|.
Dakle
(F_{n+1}F_{n-1}-F_{n}^{2})(-5)=L_{n+1}L_{n-1}-L_{n}^{2},
pa primjenom Cassinijeve formule (
5) dobivamo traženi identitet.
4Cassinijeva formula i domino
Na kraju dajemo još jednu zanimljivu interpretaciju Fibonaccijevih brojeva pomoću koje se može pokazati Cassinijeva formula (
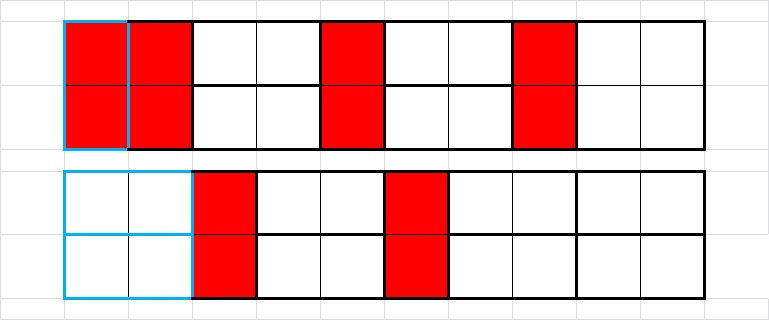
5). Radi se o popločavanju ploče dimenzije
2\times n pomoću domino pločica dimenzije
1\times 2 koje možemo postaviti vertikalno (crvena pločica) ili horizontalno (bijela pločica). Označimo s
T_{n} broj načina na koji se može izvesti.
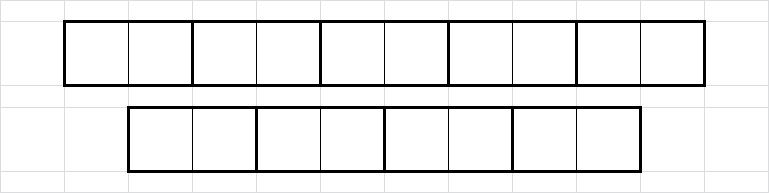
Budući da popločavanje možemo započeti ili s jednom vertikalno postavljenom pločicom ili s dvije horizontalno postavljene (vidi Sliku
2) slijedi da je
T_{n}=T_{n-1}+T_{n-2}.
Kako je
T_{1}=1 i
T_{2}=2, zaključujemo da je
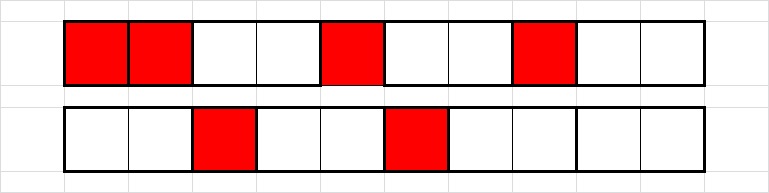
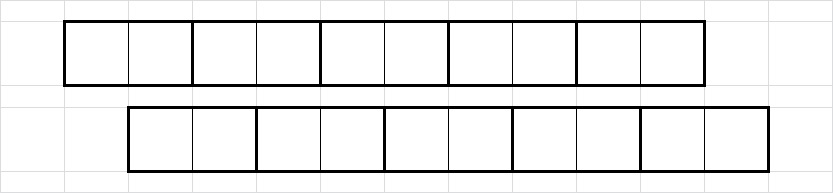
T_{n}=F_{n-1} jer imamo istu rekurziju kao za Fibonaccijeve brojeve, samo su početni (pa onda i svi ostali) članovi niza pomaknuti za jedno mjesto. Sada ćemo proučiti popločavanje dviju ploča istih dimenzija. Broj načina na koji možemo popločati te dvije ploče je
T_{n}^{2}. Zbog jednostavnosti umjesto ploče dimenzije
2\times n koju popločavamo pločicama dimenzije
1\times 2 možemo promatrati ploču dimenzije
1\times n koju popločavamo pločicama dimenzije
1\times 1 i
1\times 2 (Slika 3). Uočimo da dva popločavanja na Slici 3 upravo odgovaraju dvama popločavanjima na Slici 2.
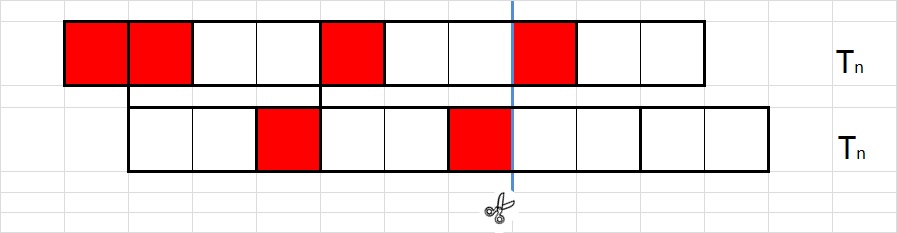
Sada donju ploču pomaknimo za jedno mjesto udesno i pogledajmo na koliko mjesta možemo 'prelomiti' i gornju i donju ploču istovremeno, a da pritom ne lomimo domino pločice. Na primjeru sa Slike
4 to se može učiniti na točno 3 mjesta. Reći ćemo da u ovom slučaju imamo 3
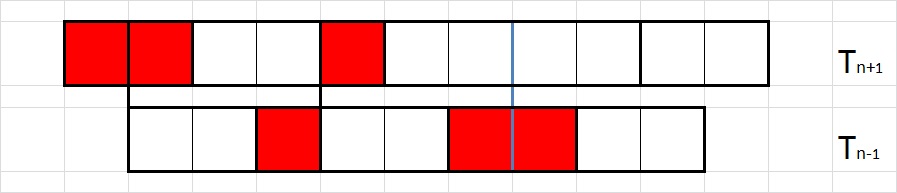
crte loma. Posljednju crtu loma označili smo plavom bojom. Sada zamijenimo dijelove ploče ('repove') koje se nalaze s desnih strana plave crte (Slika 5). Na taj način se gornja ploča povećala za točno jedno mjesto, a donja smanjila za jedno. Uočimo da se broj crta loma se nije promijenio. Općenito možemo zaključiti da postoji bijekcija između skupa svih mogućih popločavanja dviju ploča iste dimenzije
1\times n i skupa svih mogućih popločavanja dviju ploča dimenzija
1\times (n+1) i
1\times (n-1) uz pretpostavku da su to popločavanja s barem jednom crtom loma.
Sada nam preostaje prebrojati načine popločavanja u kojima se ne pojavljuje prijelom. Ukoliko je
n paran pojavit će se točno jedno takvo popločavanje dviju ploča iste dimenzije
1\times n, dok svako popločavanje dviju ploča dimenzija
1\times (n+1) i
1\times (n-1) uvijek ima crtu loma jer je broj polja na pločama neparan (pa u popločavanje moramo uključiti pločicu dimenzije
1\times 1). Točno obratno se dešava ako je
n neparan (Slika 6, 7). Stoga smo opravdali formulu
T_{n}^{2}-T_{n-1}\cdot T_{n+1}=(-1)^{n},
što uz
T_{n}=F_{n-1} upravo predstavlja Cassinijevu formulu (
5).
Bibliografija
|
[1] |
B. Bakula, Fibonaccijeve matrice i determinante, diplomski rad, PMF - Matemački odsjek, Sveučilište u Zagrebu, 2013. |
|
[2] |
A. Dujella, Fibonaccijevi brojevi, HMD, Zagreb, 2000. |
|
[3] |
T. Koshy, Fibonacci and Lucas numbers with applications, John Wiley \& Sons, 2001. |
|
[4] |
Cassini's Identity, dostupno na http://www.cut-the-knot.org/arithmetic/algebra/CassinisIdentity.shtml |
|
[5] |
Fibonacci Tilings, dostupno na http://www.cut-the-knot.org/arithmetic/combinatorics/FibonacciTilings.sh... |