Metoda konačnih elemenata je jedna od najpopularnijih numeričkih metoda za rješavanje parcijalnih diferencijalnih jednadžbi. Cilj ovog rada je na jednostavan način, kroz primjere, prezentirati metodu konačnih elemenata. U prvom dijelu rada je opisana Galerkinova metoda te je kroz jednostavan primjer skrenuta pozornost na opasnosti prilikom numeričke implementacije. U središnjem dijelu rada je opisana metoda konačnih elemenata kao poseban slučaj Galerkinove metode, a kroz primjer je dano numerički prihvatljivije rješenje primjera iz prvog dijela rada, samo što je jedan rub ostavljen slobodnim kako bi se prikazala implementacija raznih rubnih uvjeta. U završnom dijelu rada su dane neke ideje o implementaciji metode konačnih elementa na problemima koji uključuju više derivacije te par komentara vrijednih za praktičnu implementaciju.

U ovom odjeljku ćemo postaviti scenu za metodu konačnih elemenata. Započinjemo kratkim opisom Galerkinove metode. Neka je V Hilbertov prostor, a(\cdot , \cdot) : V \times V \to \mathbb{R} bilinearna forma koja je ograničena,
 

i V-eliptična,
 

te l ograničeni linearni funkcional. Promatramo problem

Prema Lax-Milgramovoj lemi, varijacijski problem (1) ima jedinstveno rješenje. Općenito govoreći, nemoguće je naći egzaktno rješenje od (1) zato što je V beskonačno dimenzionalni prostor. Prirodno je probati konstruirati aproksimaciju rješenja u konačnodimenzionalnom prostoru V_{N} \subset V. Promotrimo projekciju problema (1) na V_{N},

Uz pretpostavke da je bilinearna forma a ograničena, V - eliptična i l ograničeni linearni funkcional, opet primjenom Lax-Milgramove leme slijedi da (2) ima jedinstveno rješenje u_{N}.


Neka je \lbrace \phi_{i}\rbrace _{i=1}^{N} baza konačnodimenzionalnog prostora V_{N}, tada možemo zapisati

za neke, trenutno nepoznate, skalare \xi_{i}, i = 1,2,..,N.
Uzmimo da v \in V_{N} budu baš \phi_{i} te uvrstimo u (2). Dobivamo

Očito, prethodnu tvdnju možemo zapisati kao linearni sustav

gdje je vektor nepoznanica \mathbf{\xi} = (\xi_{j}) \in \mathbb{R}^{N}, \mathbf{K} = (a(\phi_{j},\phi_{i})) \in \mathbb{R}^{N\times N} matrica sustava te \mathbf{b} = (l(\xi_{i}))\in \mathbb{R}^{N} desna strana.


Općenito je aproksimacija u_{N} različita od rješenja u, stoga je prirodno tražiti približno rješenje u_{N} u potprostoru V_{N} što veće dimenzije. Za niz potprostora V_{N_{i}} takvih da vrijedi V_{N_{1}} \subset V_{N_{2}} \subset ... V_{N}, računamo pripadna rješenja u_{N_{i}}, i = 1,2,.... Ovaj postupak nazivamo Galerkinovom metodom. Prvi korak u dokazu konvergencije Galerkinove metode je važan i elegantan teorijski rezultat.

U slučaju kada je a(\cdot,\cdot) simetrična bilinearna forma ona definira skalarni produkt na V i njime induciranu normu \Vert v\Vert _{a} = \sqrt{a(v,v)}. Ako sada oduzimemo (2) od (1) zbog linearnosti slijedi

Vidimo da je s obzirom na novi skalarni produkt pogreška u - u_{N} ortogonalna na potprostor V_{N}. Drugim riječima, u_{N} je ortogonalna projekcija egzaktnog rješenja u na potprostor V_{N}.

Promotrimo primjenu Galerkinove metode na jednostavnom primjeru.

Iako je s teorijske strane ovaj pristup jednostavan i elegantan, neke detalje ćemo ipak morati prilagoditi kako bismo osigurali spomenuta dobra svojstva i praktičnoj izvedbi.

U prethodnom primjeru prilikom numeričke izvedbe Galerkinove metode vidjeli smo da se rješavanje linearnog rubnog problema svodi na rješavanje sustava linearnih jednadžbi. No, matrica sustava je bila gusto popunjena i loše uvjetovana. Htjeli bismo prilagoditi Galerkinovu metodu tako da u konačnici dobijemo sustav koji je dobro uvjetovan i još po mogućnosti rijetko popunjen. Ipak, za računanje svakog elementa matrice potrebno je riješiti ponekad netrivijalan integral - što je vremenski skupo ukoliko je matrica gusto popunjena. Kada radimo sa sustavima čije su matrice rijetko popunjene otvara se još jedan bonus, mogućnost uporabe iterativnih metoda. Jedan način na koji možemo riješiti prethodna dva problema jest pažljivim odabirom baze konačnodimenzionalnog prostora V_{N}. Zathjevat ćemo da je broj baznih funkcija čiji se nosači sijeku s nosačem proizvoljne bazne funkcije što manji mogući. Odlučit ćemo se za prostor V_{N} koji se sastoji od funkcija koje su po dijelovima polinomi povezani s diskretizacijom domene \Omega. Jednostavno govoreći, Galerkinova metoda uz prethodne pretpostavke na bazne funkcije postaje metoda konačnih elemenata.
Konvergencija metode konačnih elemenata može se postići povećanjem stupnja polinoma u baznim funkcijama, profinjavanjem diskretizacije domene ili čineći obje istovremeno. Ilustrirajmo sada na primjeru navedene ideje.

U nastavku promotrimo jednadžbu koja opisuje otklon žice klavira pod utjecajem sile f. Žica klavira ima dva dijela; žičanu jezgru te žicu namotanu oko nje. Uzevši to u obzir, jasno je da se takav objekt ne ponaša isključivo kao tanka žica. Žica klavira vibrira dijelom zbog napetosti, a dijelom zbog same čvrstoće žice. Iz tog razloga modelu dodajemo član koji opisuje ponašanje tankog štapa.

Slaba formulacija problema je

gdje je V = H_{0}^{2}(\langle0,1\rangle). Ako želimo odabrati V_{h}, takav da je V_{h} \subset V, onda svaka funkcija u V_{h} mora bit barem klase \mathcal{C}^{1}. Pretpostavimo da se V_{h} sastoji od po dijelovima polinoma stupnja manjeg ili jednakog p. Uvjet da su funkcije u V_{h} klase \mathcal{C}^{1} nameće 2(N-1) uvjeta, a rubni uvjeti još 4 uvjeta. Sve skupa imamo

stupnja slobode da odaberemo bazne funkcije sa što manjim nosačem. Jasno je da je najmanji dozvoljeni p = 2. Međutim odlučit ćemo se za p = 3 da bismo povećali broj stupnjeva slobode za odabir baznih funkcija. Za p =3 prostor konačnih elemenata je

Možemo konstruirati bazne funkcije s malim nosačima koristeći uvjete interpolacije

Kako bismo izbjegli tehničke komplikacije, poželjno je raditi na referentnom elementu. Ideja je sav posao obaviti na jednom elementu, tzv. referentnom elementu, a onda postignuto preslikati na ostale elemente. Neka je I_{0} = \langle 0, 1\rangle, preslikavanje

je bijekcija. Na referentnom elementu I_{0} konstruiramo polinome trećeg stupnja koji zadovoljavaju interpolacijske uvjete

Jednostavnim računom određujemo da su tražene funkcije

Sad možemo odrediti bazne funkcije

i

Kao i u prethodnim primjerima, želimo formulirati sustav linearnih jednadžbi. Koeficijente matrice sustava računat ćemo preko referentnog elementa, npr.

koristeći definiciju baznih funkcija i funkcije F_{i} možemo izračunati

Ostale elemente matrice možemo izračunati analogno, a tako dobivena matrica će biti petdijagonalna. Komentirajmo za kraj da je za višedimenzionalne probleme tehnika referentnog elementa neophodna, kako za teorijsku analizu greške tako i za praktičnu implementaciju. Valja primijetiti da smo u prethodnom jednodimenzionalnom primjeru zahtijevali da funkcije iz V_{h} budu polinomi trećeg stupnja kako bismo postigli da funkcije iz V_{h} \subset V budu klase \mathcal{C}^{1}. U višim dimenzijama je potreban još veći stupanj polinoma kako bismo to postigli. Jedan način kako je moguće riješiti taj problem jest korištenjem nekonformnih elemenata ([5]).
Za sam kraj, ostavljamo čitatelju jedan programerski podhvat.


Zadatak. Napravite programsku izvedbu metode konačnih elemenata za sljedeći problem

Egzaktno rješenje ovog problema je

Zahvaljujem se prof.dr.sc. Josipu Tambači na detaljnom čitanju ovog članka i korisnim savjetima.

[1] Atkinson, Han. Theoretical Numerical Analysis: a functional framework. Vol 19. Springer, 2009.
[2] Dhatt, Gouri i Touzot, Gilbert. Finite Element Method. John Willey and Sons, 2012.
[3] Brenner, Susanne i Carstensen, Carsten. Encyclopedia of Computational Mechanics. Chapter 4, Finite Element Methods. John Wiley and Sons, 2004.
[4] Jurak, Mladen. Praktikum primijenjene matematike II. Skripta, PMF Matematički odsjek, 2008.

[5] Ciarlet, Philippe G. The finite element method for elliptic problems. Elsevier, 1978.

Krešimir Burazin, Zoran Tomljanović i Ivana Vuksanović

 

Odjel za matematiku
Sveučilište Josipa Jurja Strossmayera u Osijeku
Trg Lj. Gaja 6
31000, Osijek
[email protected] (K. Burazin)
[email protected] (Z. Tomljanović)
[email protected] (I. Vuksanović)

Sažetak:
U radu su opisane vibracije sustava koji se sastoji od jedne mase, opruge i viskoznog prigušivača, te sustava od dvije mase, tri opruge i viskoznog prigušivača. Posebno je naglašen problem pronalaska optimalnog prigušenja slobodnih vibracija s obzirom na kriterij spektralne apscise i kriterij minimizacije ukupne energije sustava. Prikazane su i prisilne vibracije harmonijskog oscilatora, s naglaskom na pojavi rezonancije. Također su dani primjeri nekih građevina kod kojih su vibracije imale katastrofalne posljedice, te primjeri građevina kod kojih su te vibracije smanjene upotrebom raznih vrsta prigušivača.

Ključne riječi:

vibracije, harmonijski oscilator, rezonancija, prigušenje, optimalno prigušenje




U fizici se vibracija definira kao gibanje mase ili sustava povezanih masa oko  položaja ravnoteže. Ovdje se zapravo misli na mehaničke vibracije, odnosno na vibracije dinamičkih sustava. Međutim, sam pojam vibracije možemo shvatiti i u širem kontekstu i vjerojatno ga je, na intuitivnoj razini, najlakše usvojiti kroz razne primjere vibracionog gibanja, poput kretanja klatna sata, vibriranja žica glazbenih instrumenata, vibriranja kotača automobila, vibriranja membrane zvučnika, kucanja srca, vibriranja raznih mehaničkih uređaja (motora automobila, perilice za rublje, miksera), osciliranja serijskog strujnog kruga, vibriranja raznih građevinskih struktura (nebodera, mostova), i mnogih drugih.

Kroz ove primjere možemo uočiti da je vibracija jedan od najrasprostranjenijih oblika gibanja u prirodi. Zapravo, ukoliko probate naglas pročitati ovu rečenicu, vibriranje vaših glasnica će vam omogućiti da proizvedete potrebne zvukove, dok će vibriranje bubnjića u vašem uhu omogućiti da čujete ono što ste izgovorili.

Ljudi su se počeli zanimati za vibracije već od pojave prvih glazbenih instrumenata. Prvi koji je na znanstvenoj osnovi počeo promatrati glazbu i zvukove bio je grčki filozof i matematičar Pitagora. Kasnije su se tom vrstom gibanja bavili mnogi matematičari i fizičari, između ostalih G. Galilei, I. Newton, B. Taylor, D. Bernoulli, J. D'Alambert, L. Euler, G. R. Kirchoff, te mnogi drugi.

Već iz gore nabrojanih primjera možemo uočiti da su neke vibracije poželjne, dok neke baš i nisu. Od poželjnih vibracija, osim onih očitih koje su bitne za sam život čovjeka, poput kucanja srca i vibriranja glasnica, izdvajamo razne uređaje koji rade na principu vibracija, poput glazbenih instrumenata, kućanskih aparata (perilica rublja, mikser, shaker), satova, građevinskih strojeva (pneumatski čekić,  žaba, raketa), masažera i mnogih drugih. Nažalost, većina vibracijskih gibanja je ipak nepoželjna, i većina inženjera i znanstvenika koji se bave vibracijama zapravo pokušavaju smanjiti neželjene vibracije, odnosno bave se  prigušenjem vibracija. Neželjene vibracije se javljaju u velikom broju mehaničkih uređaja, poput turbina, pumpi, kompresora, aviona i automobila. Prevelike vibracije unutar takvih sustava proizvode neželjene zvukove, mogu dovesti do oštećenja dijelova sustava, te na kraju i do kvara, dok kod ljudi koji se nalaze u blizini izazivaju neugodu, umor i općenito gubitak efikasnosti.

Manje je poznato da i velike građevine poput mostova, nebodera i katedrala također vibriraju. Štoviše, te vibracije znaju biti prilično velike pa i uzrokovati oštećenja ili čak rušenje građevine (u zadnjem poglavlju je dano nekoliko primjera vibriranja građevina). Pri tome je izuzetno opasna pojava tzv.  rezonancije kada može doći do velikih vibracija iako sile koje djeluju na sustav nisu velike po apsolutnoj vrijednosti. Stoga se na razne načine pokušavaju smanjiti vibracije, najčešće korištenjem raznih prigušivača koji onda te vibracije svode na prihvatljivu razinu.

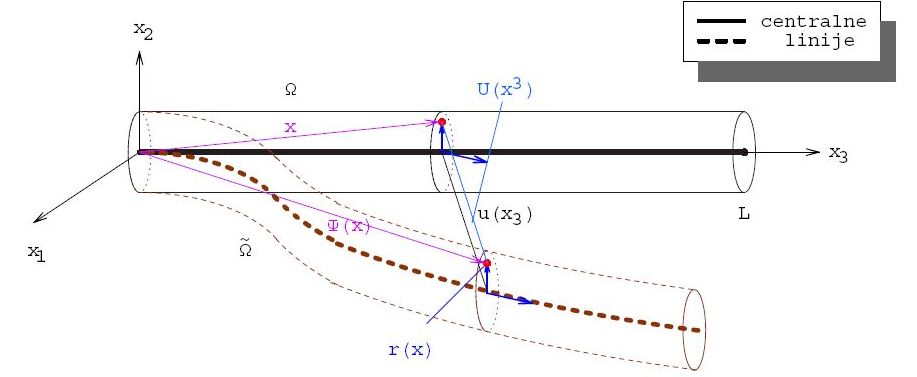
Matematički modeli kojima se opisuje vibracijsko gibanje obično vode na parcijalne diferencijalne jednadžbe koje su dosta složene za proučavanje, pa problemi prigušenja vibracija predstavljaju veliki izazov za znanstvenike i inženjere. Međutim, mnoge fenomene koji se pojavljuju u ovakvim sustavima možemo primijetiti već i u najjednostavnijem jednodimenzionalnom modelu harmonijskog oscilatora. U radu ćemo prikazati upravo takve vibracije promatrajući jednostavan fizikalni problem - sustav masa i opruga s jednim stupnjem slobode.

Primjeri koje dajemo u petom poglavlju pokazuju kako vibracije mogu imati razorno djelovanje na građevinske objekte. Također navodimo primjere građevina kod kojih je smanjen utjecaj vibracija te objašnjavamo na koji je način to učinjeno.




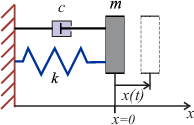
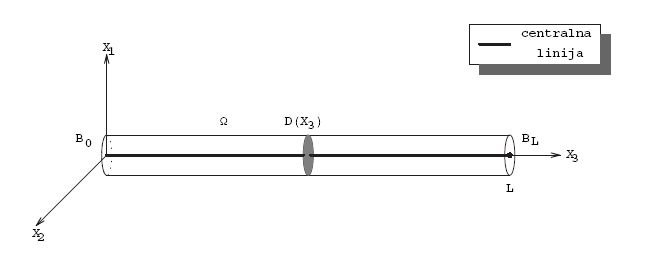
Za početak promotrimo sustav prikazan na Slici 2.1: radi se o sustavu jedne mase m\gt 0 pričvršćene elastičnom oprugom konstante elastičnosti k\gt 0 za fiksnu podlogu, s tim da je na masu istovremeno pričvršćen i prigušivač koji pruža otpor gibanju mase proporcionalan brzini gibanja, s konstantom proporcionalnosti (prigušenja) c\gt 0. Pretpostavimo da na sustav u trenutku t djeluje i vanjska sila f(t) u smjeru osi x, te da ne djeluju nikakve druge sile osim već navedenih (nema gravitacije, otpora zraka, trenja i sl.). Također pretpostavljamo da se gibanje vrši samo u smjeru osi x, te s x(t) označimo otklon tijela u trenutku t od ravnotežnog položaja. Cilj nam je pronaći položaj tijela u svakom trenutku t, odnosno pronaći funkciju pomaka x:\langle 0,\infty \rangle \rightarrow {\textbf{R}} na osnovu poznatih sila koje dijeluju na tijelo i poznatog  stanja tijela u trenutku t=0 (početni položaj i početna brzina tijela). Najprije ćemo iz Newtonovog drugog zakona: \displaystyle\ F=ma=m\frac{dv}{dt}=m\frac{d^{2}x}{dt^{2}}, gdje je a akceleracija, v brzina tijela, a F zbroj svih sila koje djeluju na masu m, odrediti jednadžbu gibanja tijela. Naime, sile koje u trenutku t djeluju na masu su

\bullet	{sila opruge}, koja je prema Hookeovom zakonu proporcionalna otklonu tijela od položaja mirovanja, odnosno jednaka -kx(t);
\bullet	{sila prigušenja} jednaka - cx'(t);
\bullet	{vanjska sila} f(t).

Stoga drugi Newtonov zakon postaje odnosno dobivamo jednadžbu harmonijskog oscilatora sa prigušenjem: To je diferencijalna jednadžba za nepoznatu funkciju x i ukoliko ju podijelimo s m\gt 0, dobivamo ekvivalentnu jednadžbu gdje su \displaystyle\ \bar{c}=\frac{c}{m} i \displaystyle\ \omega_{0}^{2}=\frac{k}{m}, \omega_{0}\gt 0.

Taj tip diferencijalne jednadžbe naziva se linearna diferencijalna jednadžba drugog reda s konstantnim koeficijentima i dobro je poznato kako se rješava (vidi [1] za više detalja). Preciznije, ta jednadžba ima beskonačno mnogo rješenja koja se mogu eksplicitno zapisati, s tim da oblik rješenja ovisi o rješenjima pripadne karakteristične jednadžbe koja su dana s Razlikujemo tri moguća slučaja:
A) \lambda_{1}, \lambda_{2}\in {\textbf{R}} i \lambda_{1}\not= \lambda_{2}, tj.  \bar{c}\gt 2\omega_{0}, odnosno c\gt 2\sqrt{km}, i tada je gdje su C_{1}, C_{2} \in {\textbf{R}} proizvoljni, dok je x_{p} partikularno rješenje jednadžbe (2), tj.  jedno (bilo koje) rješenje te jednadžbe (ono ovisi o f i ovdje nećemo previše govoriti o metodama za pronalazak partikularnog rješenja; vidi [1]).

B) \lambda_{1},\lambda_{2} \in {\textbf{R}} i \lambda_{1}= \lambda_{2}, tj.  \bar{c}=2\omega_{0}, odnosno c=2\sqrt{km}, i tada je gdje su C_{1}, C_{2} \in {\textbf{R}} proizvoljni, a x_{p} partikularno rješenje jednadžbe (2).

C) \lambda_{1}, \lambda_{2}\not\in {\textbf{R}}, tj.  \bar{c}\lt 2\omega_{0}, odnosno c\lt 2\sqrt{km}. U tom slučaju je \lambda_{1,2} = -\frac{\bar{c}}{2} \pm \bar{\omega} i, gdje je \bar{\omega} = \sqrt{\omega_{0}^{2}- \bar{c}^{2}/4}\in {\textbf{R}}\setminus \lbrace 0\rbrace, i tada je gdje su C_{1}, C_{2} \in {\textbf{R}} proizvoljni, a x_{p} partikularno rješenje jednadžbe (2). Lako se može provjeriti da u ovome slučaju rješenje možemo zapisati u obliku gdje su A\in\textbf{R} i \varphi\in [-\pi, \pi\rangle određeni s Napomenimo još da je za f\equiv 0 u sva tri slučaja trivijalno partikularno rješenje dano s x_{p}\equiv 0.

Uočimo da se u svakom od gore navedenih slučajeva u formuli za rješenje pojavljuju dvije proizvoljne realne konstante C_{1} i C_{2}. To ujedno znači da ta jednadžba ima beskonačno mnogo rješenja, odnosno da funkciju pomaka x nije moguće odrediti samo iz jednadžbe. Fizikalno gledano to je i očekivano, jer da bi se poznavao pomak u trenutku t nije dovoljno imati informacije samo o silama koje dijeluju na masu m. Potrebno je poznavati i stanje u kojem se masa nalazi u početnom trenutku, odnosno početni položaj x(0) i početnu brzinu x'(0) mase m.

U sustavu ne moraju biti prisutne sve navedene sile, pa tako u slučaju kada nema djelovanja vanjske sile (f\equiv 0) govorimo o slobodnim vibracijama, dok u suprotnom govorimo o prisilnim vibracijama. Isto tako, ukoliko u sustavu nema prigušivača (c =0) onda kažemo da je sustav neprigušen, a u suprotnom da je prigušen. U nastavku ćemo razmotriti slobodne vibracije, dok će o prisilnim vibracijama biti više riječi u zadnjem poglavlju.



Pretpostavimo najprije da na sustav ne djeluju nikakve vanjske sile i da nema prigušenja, tj. da je f\equiv 0 i c=0. Tada jednadžba (2) glasi x''(t)+ \omega_{0}^{2}x(t)=0, pripadna karakteristična jednadžba je \lambda^{2}+\omega_{0}^{2} =0, a njena rješenja su \lambda_{1,2}=\pm \omega_{0}i. 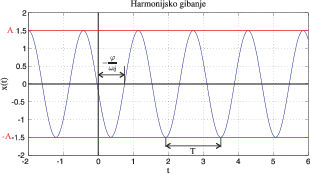Ovo je očito slučaj C, pa je rješenje dano s gdje se konstante A i \varphi lako odrede iz početnog pomaka x(0)=x_{0} i početne brzine x'(0)=v_{0}: Primijetimo da funkcija x poprima vrijednosti u segmentu [-A, A], te da je periodična, s temeljnim periodom \displaystyle\ T=\frac{2\pi}{\omega_{0}}. 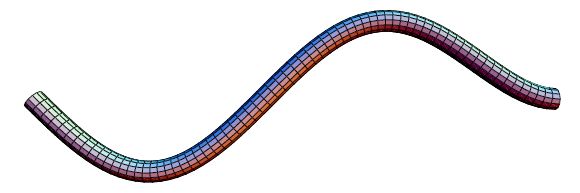Ovakvo gibanje naziva se harmonijsko gibanje; A nazivamo amplituda, \varphi fazni pomak, a \omega_{0} vlastita frekvencija sustava. Na Slici 2.2 prikazano je jedno ovakvo gibanje za funkciju x(t)=1.5 \sin(4 t-3).


Ukoliko je u sustavu prisutno prigušenje c\gt 0, a na njega ne djeluje nikakva vanjska sila, onda je desna strana jednadžbe gibanja (2) jednaka nuli, pa slučajevi A, B, C vode na sljedeće:

A) Ako je c\gt 2\sqrt{km} (veliko prigušenje), onda je gdje su \lambda_{1,2} dani s (3), a C_{1} i C_{2} se lako izračunaju iz početnih uvjeta:
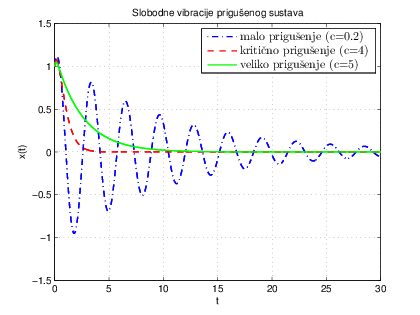
Uočimo da su \lambda_{1,2} \lt 0 pa je x padajuća funkcija koja teži prema nuli za velika vremena t. Ovakav oblik gibanja nazivamo pregušene oscilacije i prikazan je na Slici 2.3 zelenom bojom.

B) Slučaj c=2\sqrt{km} nazivamo kritično prigušenje i tada je (nakon što se izračunaju C_{1} i C_{2} iz početnih uvjeta) Ovakvo gibanje tijela nazivamo kritično prigušenje i jedno takvo prigušenje prikazano je na Slici 2.3 crvenom bojom.
C) Konačno, slučaj c\lt 2\sqrt{km} vodi na gdje je \bar{\omega} = \sqrt{\omega_{0}^{2}- \bar{c}^{2}/4}\in {\textbf{R}}\setminus \lbrace 0\rbrace, a konstante A i \varphi su određene s Ovakav slučaj gibanja nazivamo malo prigušenje. Veličina \displaystyle\ Ae^{-\frac{\bar{c}}{2}t} predstavlja amplitudu osciliranja i ovisi o vremenu, a \varphi fazni pomak. Uočavamo da ovo gibanje nije periodičko jer amplitude nisu konstante, već se tijekom vremena smanjuju, tj. kada vrijeme teži beskonačnosti, pomak tijela od ravnotežnog položaja teži nuli. Stoga se u ovom slučaju veličina \displaystyle\ T=\frac{2\pi}{\bar{\omega}} naziva prividnim periodom gušenja. Graf ovakvog gibanja je prikazan na Slici 2.3 plavom bojom.

Kritično prigušenje se naziva i optimalnim prigušenjem jer odgovara prigušenju koje (u nekom smislu) optimalno prigušuje sustav. Optimalnost prigušenja bit će detaljnije diskutirana u nastavku teksta. Stoga prigušenja koja odgovaraju parametrima manjim od optimalnog nazivamo malim prigušenjima, dok veliko prigušenje odgovara parametrima koji su veći od kritičnog prigušenja.


S ciljem poopćenja harmonijskog oscilatora na problem titranja više masa, promotrit ćemo sustav dviju masa koje titraju. Sustav je opisan na Slici 4 pri čemu su mase m_{1} i m_{2} međusobno povezane oprugom elastičnosti k_{2}, dok su za fiksnu podlogu povezani pripadnim oprugama elastičnosti k_{1} i k_{3}. Pretpostavit ćemo da je na prvu masu pričvršćen i prigušivač s konstantom prigušenja c, te da na mase ne djeluju dodatne sile osim navedenih (nema vanjske sile, tj. proučavamo slobodne oscilacije. Nadalje, pretpostavimo da se gibanje vrši samo u jednom smjeru te redom s x_{1}(t) i x_{2}(t) označimo otklone masa m_{1} i m_{2} od položaja ravnoteže.

Da bismo opisali gibanje masa primijetimo najprije da su promjene duljina opruga k_{1}, k_{2} i k_{3} redom jednake x_{1}, x_{2}-x_{1} i -x_{2}. Sada slično kao i u slučaju harmonijskog oscilatora, uzevši u obzir drugi Newtonov zakon i Hookeov zakon, dobivamo sustav jednadžbi koji opisuje gibanje prve i druge mase: To je sustav dvije obične diferencijalne jednadžbe s nepoznanicama x_{1} i x_{2}. Radi jednostavnije analize taj sustav ćemo zapisati u matričnom obliku: gdje su nepoznanice u novom vektoru \mathsf{x}(t)=\left[ \begin{array}{c} x_{1}(t) \\ x_{2}(t) \\ \end{array} \right], a matrice su zadane s Direktnim množenjem lako se može provjeriti da je polazni sustav uistinu ekvivalentan s (6). Matrica \textbf{M} obično se naziva matrica mase, \textbf{K} matrica krutosti, dok matricu \textbf{C} nazivamo matricom prigušenja.

Sustavu (6) dodaju se i jednakosti koje određuju stanje tijela u trenutku t=0, odnosno početni položaj i početna brzina tij\'ela:

U početku promotrimo neprigušeni slučaj, odnosno slučaj kada je c=0. Kako bismo povezali ovaj slučaj sa slučajem harmonijskog oscilatora, moramo sustav (6) zapisati u pogodnijem obliku. U tu svrhu potrebno je uvesti pojam svojstvenih vrijednosti i svojstvenih vektora matričnog para: za vektor {\boldsymbol{\phi}} kažemo da je svojstveni vektor matričnog para (\textbf{A}, \textbf{B}) kojem pripada svojstvena vrijednost \mu \in {\textbf{C}} ako vrijedi \textbf{A}{\boldsymbol{\phi}} = \mu \textbf{B} {\boldsymbol{\phi}}, {\boldsymbol{\phi}} \neq \mathsf{0}. Poznato je da se svojstvene vrijednosti para mogu izračunati kao nultočke karakterističnog polinoma p(\mu)=\det (\textbf{A}-\mu \textbf{B}) (vidi [8]). Uočimo da ćemo za \textbf{B}=\textbf{I} dobiti standardni svojstveni problem.

Kod titrajnih problema vrlo važnu ulogu igraju svojstvene vrijednosti matričnog para (\textbf{K}, \textbf{M}), odnosno zanima nas svojstveni problem Za matrice \textbf{M} i \textbf{K} dane u (7), lako se može provjeriti da karakteristični polinom glasi pa se računanje svojstvenih vrijednosti svodi na rješavanje kvadratne jednadžbe, nakon čega se svojstveni vektori mogu odrediti rješavanjem sustava dvije jednadžbe s dvije nepoznanice, odnosno sustava (9). Lako se može vidjeti da su te svojstvene vijednosti pozitivne pa ih se može zapisati kao \mu_{i}=\omega_{i}^{2}, \omega_{i} \gt 0, i=1,2. Štoviše, pripadni svojstveni vektori {\boldsymbol{\phi}}_{1} i {\boldsymbol{\phi}}_{2} se mogu odabrati tako da vrijedi gdje je
Gore navedene tvrdnje vrijede i u nekim općenitijim situacijama (sustav više masa) a posljedica su toga što su \textbf{M} i \textbf{K} simetrične pozitivno definitne matrice.

Naime, za proizvoljnu simetričnu pozitivnu matricu \textbf{B} postoji matrica \textbf{C} takva da je \textbf{B}=\textbf{C}^{2}, takvu matricu \textbf{C} zovemo korijenom matrice \textbf{B} i označavamo ju s \textbf{B}^{\frac{1}{2}}. Budući da je matrica \textbf{M} simetrična pozitivno definitna tada postoji simetrična pozitivno definitna matrica \textbf{M}^{\frac{1}{2}}. Tada je matrica \textbf{K}_{1}=\textbf{M}^{-\frac{1}{2}} \textbf{K} \textbf{M}^{-\frac{1}{2}} također simetrična pozitivno definitna, stoga za nju postoji realna ortogonalna matrica \textbf{Q} i dijagonalna matrica {\boldsymbol{\Lambda}} tako da je gdje je {\boldsymbol{\Lambda}} matrica koja na dijagonali sadrži upravo svojstvene vrijednosti matrice K_{1} koje su pozitivne zbog pozitivne definitnosti matrice \textbf{K}_{1}.

Sada za matricu {\boldsymbol{\Phi}} definiranu s {\boldsymbol{\Phi}}:=\textbf{M}^{-\frac{1}{2}}\textbf{Q} direktnim uvrštavanjem možemo provjeriti da su zadovoljene jednakosti (10). Zaista, koristeći simetričnost matrice \textbf{M}^{\frac{1}{2}} i ortogonalnost matrice \textbf{Q} slijedi dok iz (12) dobivamo Budući da je {\boldsymbol{\Lambda}} dijagonalna matrica s pozitivnim elementima na dijagonali, to ju možemo zapisati kao {\boldsymbol{\Omega}}^{2}. Više detalja vezano uz navedene tvrdnje može se pronaći u [7, 8].

Navedene svojstvene vrijednosti i svojstveni vektori imaju veliku važnost u analizi titranja promatranog sustava. Naime, \omega_{1} i \omega_{2} se nazivaju vlastite ili svojstvene frekvencije neprigušenog sustava, a svojstveni vektori {\boldsymbol{\phi}}_{1}, {\boldsymbol{\phi}}_{2} u fizici se često zovu prvim, odnosno drugim modom titrajnog sustava, i možemo reći da oni određuju smjer gibanja pripadnih masa.

Nadalje, ako uzmemo supstituciju \mathsf{\hat{x}(t)}=\Phi^{-1} \mathsf{x}(t) u sustavu (6) (za \textbf{C}=\textbf{0}) te pomnožimo jednadžbu s lijeva s {\boldsymbol{\Phi}}^{T} i iskoristimo jednakosti dane u (10) dobit ćemo sustav Možemo primjetiti da smo neprigušeni problem zapisali tako da smo (u novim koordinatama) dobili titranja harmonijskih oscilatora s neprigušenim frekvencijama \omega_{1} i \omega_{2}. Stoga, postupajući analogno kao u slučaju neprigušenog harmonijskog oscilatora, dobivamo za i=1,2, gdje se konstante A_{i} i \varphi_{i} odrede iz početnih uvjeta (8), odnosno uz spomenutu supstituciju imamo uvjete Odavde, koristeći formule (5) dobivamo
Na kraju, ako iskoristimo da je \mathsf{x}(t)={\boldsymbol{\Phi}}\mathsf{\hat{x}}(t) dobit ćemo rješenje \mathsf{x}(t) u sljedećem obliku


Da bismo riješili problem s prigušenjem najprije ćemo naš sustav jednadžbi (6) zapisati u obliku sustava diferencijalnih jednadžbi prvog reda. Naime, uz već spomenutu supstituciju \mathsf{x}(t)={\boldsymbol{\Phi}}\mathsf{\hat{x}}(t) te dodatne supstitucije \mathsf{y_{1}}(t)= {\boldsymbol{\Omega}} \mathsf{\hat{x}}(t) i \mathsf{y_{2}}(t)=\mathsf{\hat{x}}'(t), sustav (6) možemo zapisati kao sustav gdje su a matrice {\boldsymbol{\Omega}} i {\boldsymbol{\Phi}} dane u (11). Uočimo da je za sustav dviju masa \textbf{A} matrica reda 4, dok je nepoznata funkcija \mathsf{y} vektorska funkcija koja za kodomenu ima \textbf{R}^{4}. Napomenimo i da problem harmonijskog oscilatora sa prigušenjem možemo riješiti na ovaj način, pri čemu bi \textbf{A} bila reda 2, a \mathsf{y} bi za kodomenu imala \textbf{R}^{2}.

Koristeći matrični račun rješenje dobivenog sustava možemo zapisati u obliku (vidi [1]) gdje vektor \mathsf{y}_{0} sadrži informacije o početnim uvjetima, a matrica e^{\textbf{A}t} je definirana pomoću sume reda potencija \displaystyle e^{\textbf{A}t}=\sum_{j=0}^{\infty} \frac{\textbf{A}^{j}t^{j}}{j!} (vidi [1] i [8] za detalje). Iako efikasan izračun matrice e^{\textbf{A}t} prelazi okvire ovog rada, napomenimo da se ona može relativno jednostavno izračunati ukoliko je matrica \textbf{A} u nekoj od jednostavnijih formi, na primjer u Jordanovoj kanonskoj formi.

Kada se nađe \mathsf{y}, onda se lako izračuna \mathsf{x}:



U ovome poglavlju želimo analizirati optimalno prigušenje sustava dvije mase te harmonijskog oscilatora (iako mnoge tvrdnje koje ćemo ovdje izreći vrijede i za općenitije sustave više masa). Jasno, najprije moramo precizirati što mislimo pod pojmom optimalno prigušenje. 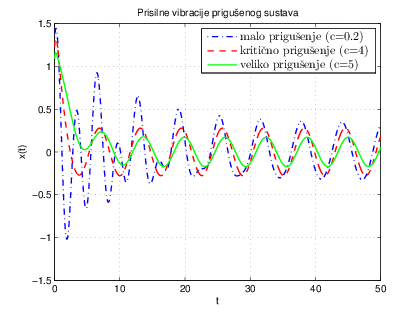Na intuitivnoj razini možemo to ovako zamišljati: vibracije u našem sustavu su neželjene, te za dane mase i koeficijente elastičnosti želimo odrediti najbolje prigušenje c koje će osigurati najbolje (optimalno) smirivanje svih komponenti (x_{1} i x_{2}). 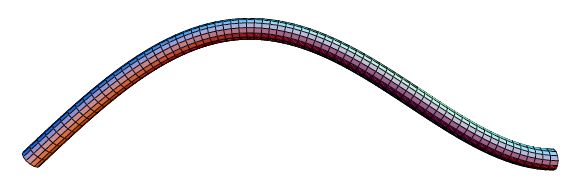Na primjer, na Slici 1 vidimo titranje prigušenog harmonijskog oscilatora koje odgovara raznim prigušenjima, te se možemo pitati koje prigušenje će nam biti najbolje (optimalno). Da bismo mogli odgovoriti na to pitanje najprije trebamo precizirati kriterije optimalnosti koji su u skladu s našim intuitivnim poimanjem smirivanja svih komponenti sustava, te konačno i pronaći optimalno prigušenje s obzirom na dani kriterij.

U primjeni postoji više kriterija, a mi ćemo navesti dva kriterija koja se često koriste (u obadva matrica \textbf{A} dana s (14) ima važnu ulogu):

\bullet	[i)] kriterij spektralne apscise
\bullet	[ii)] kriterij minimizacije ukupne energije sustava.

Kriterij spektralne apscise za optimalno prigušenje c uzima ono koje minimizira funkciju gdje su \lambda_{k} svojstvene vrijednosti matrice \textbf{A}. Uočimo da matrica \textbf{A} zaista ovisi o matrici \textbf{C}, odnosno o prigušenju c, pa stoga i njezine svojstvene vrijednosti možemo shvatiti kao funkcije prigušenja c. To znači da je s (15) zaista dobro definirana funkcija koja ovisi o prigušenju c, pa ima smisla tražiti njezin minimum.

Geometrijski gledano, ovaj kriterij nam kaže da je optimalno prigušenje upravo ono za koje su svojstvene vrijednosti što više lijevo u kompleksnoj ravnini.

U ovome trenutku ostavljamo nejasnom fizikalnu interpretaciju ovog uvjeta optimalnosti. Naime, iz gore navedenog nije jasno za što je takav kriterij odabran i u kojem smislu je takvo prigušenje optimalno. To ćemo pojasniti na primjeru harmonijskog oscilatora u sljedećem potpoglavlju.

Kriterij minimizacije ukupne energije sustava za optimalno prigušenje c uzima ono koje minimizira ukupnu energiju sustava definiranu sa gdje je E(t;\mathsf{y}_{0}) ukupna energija sustava u trenutku t, odnosno zbroj potencijalne i kinetičke energije u trenutku t: a \mathsf{y}_{0} sadrži informacije o početnim uvjetima.

Kriterij minimizacije ukupne energije intuitivno je jasan i fizikalno odgovara općenitoj ideji minimizacije energije koja se pojavljuje u raznim problemima sa fizikalnom pozadinom.

Budući da totalna energija ovisi o početnim uvjetima sadržanim u vektoru \mathsf{y}_{0}, uzimanjem usrednjenja po svim jediničnim početnim uvjetima može se pokazati (vidi npr. [5, 8]) da se ovaj kriterij svodi na minimizaciju traga matrice \textbf{X} po svim prigušenjima c, pri čemu je \textbf{X} rješenje matrične jednadžbe a matrica \textbf{A}, kao i prije, dana s (14).

Ta matrična jednadžba naziva se Ljapunovljeva jednadžba te ima veliku primjenu u teoriji upravljanja. Također uočimo da je u slučaju sustava dvije mase matrica \textbf{X} reda 4, dok je u slučaju harmonijskog oscilatora reda 2. Za matricu \textbf{A} koja ima svojstvene vrijednosti u lijevoj poluravnini kompleksne ravnine, može se pokazati da postoji jedinstveno rješenje Ljapunovljeve jednadžbe (sjetimo se da smo i kod spektralne apscise svojstvene vrijednosti pomicali što više lijevo).

Napomenimo da za ovaj kriterij postoji teorijski rezultat o optimalnom prigušenju pri čemu promatramo općenitu matricu prigušenja \textbf{C} (ne nužno oblika kao u (7)). Naime, ako bismo u jednadžbi (6) tražili optimalan \textbf{C}\in \textbf{R}^{2\times 2} za koji je \mathrm{trace}{\textbf{X}(\textbf{C})} minimalan, onda je poznato (npr. vidi [5]) da se minimum postiže za koji se stoga često naziva kritičnim ili optimalnim prigušenjem. Istaknimo da navedeni razultat vezan uz \textbf{C}_{opt} vrijedi i općenito za sustav određen matricama n-tog reda. S druge strane, zbog fizikalne pozadine problema matrica prigušenja \textbf{C} je obično specijalne strukture (npr. kao u (7)), pa se stoga u praksi dani minimum općenito ne može postići. Međutim, za neke posebne slučajeve, poput harmonijskog oscilatora može se postići, što ćemo u nastavku i pokazati.


Kada smo analizirali gibanja harmonijskog oscilatora već smo komentirali kako izgleda titranje u ovisnosti o raznim prigušenjima (vidi Sliku 1). U ovom ćemo poglavlju pokazati koliko iznosi optimalno prigušenje u slučaju harmonijskog oscilatora za kriterij spektralne apscise i za kriterij minimizacije ukupne energije sustava.

Radi potpunosti navest ćemo kako bi glasila jednadžba (13) u slučaju harmonijskog oscilatora. Naime, matrice M, C i K bile bi jednake skalarima (stoga ih ne pišemo masnim slovima), te uz oznake iz prvog poglavlja imali bismo M=m, C=c i K=k te za \Phi i \Omega iz (11) vrijedilo bi \Phi=\frac{1}{\sqrt{m}} i \Phi^{T} K \Phi = \Omega^{2}=\omega_{0}^{2}=\frac{k}{m} (odmah vrijedi i \Phi^{T} M\Phi=1). Tada bi sustav prvog reda za harmonijski oscilator glasio \mathsf{y}'(t)=\textbf{A} \mathsf{y}(t) pri čemu su funkcije \mathsf{y} i \textbf{A} dane s gdje je \displaystyle\ \bar{c}=\frac{c}{m}. Lako se može provjeriti da su svojstvene vrijednosti matrice \textbf{A} jednake nultočkama \lambda_{1,2} danim s (3).

Prisjetimo se da je kod kriterija spektralne apscise optimalno prigušenje ono za koje su svojstvene vrijednosti pripadne matrice \textbf{A} najviše moguće lijevo u kompleksnoj ravnini, odnosno želimo da je realni dio svojstvenih vrijednosti negativan i što veći po apsolutnoj vrijednosti.

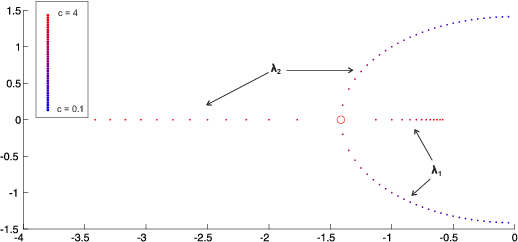
Slika 5 grafički prikazuje kako se svojstvene vrijednosti, u slučaju harmonijskog oscilatora, mijenjaju u ovisnosti o prigušenju c pri čemu se c mijenja od 0.1 do 4. Kretanje svojstvenih vrijednosti matrice \textbf{A} prikazano je tako da se prigušenje mijenja od malog prigušenja 0.1 pa do velikog prigušenja koji iznosi 4. Kretanje je ilustrirano promjenom boje svojstvenih vrijednosti tako da su svojstvene vrijednosti za prigušenje 0.1 obojane sa plavom bojom, a kako parametar prigušenja raste prema broju 4 tako se boja mijenja prema crvenoj.

Možemo zaključiti da ako je c mali i ako c raste, onda su svojstvene vrijednosti kompleksne i pomiču se lijevo u kompleksnoj ravnini sve do trenutka kad svojstvena vrijednost postane dvostruka i realna te negativna. Nakon toga svojstvene vrijednosti su realne pri čemu jedna svojstvena vrijednost raste, a druga pada. Stoga, možemo zaključiti da će svojstvene vrijednosti biti najviše lijevo upravo u trenutku kad su svojstvene vrijednosti realne i dvostruke, a to je za c_{opt}=2\sqrt{km}= 2\sqrt{2}, što odgovara slučaju kritičnog prigušenja. Upravo se zato taj slučaj i naziva kritičnim (optimalnim) prigušenjem. Svojstvene vrijednosti koje odgovaraju kritičnom prigušenju označene su crvenim krugom.

Sada je vrijeme da pogledamo fizikalnu interpretaciju kriterija spektralne apscise na primjeru harmonijskog oscilatora: svojstvene vrijednosti \lambda_{1}, \lambda_{2} matrice \textbf{A} se direktno pojavljuju u formulama za funkciju pomaka danim u poglavlju 2.2. Neovisno o tome o kolikom je prigušenju riječ, pažljiviji pogled na te formule će otkriti da na amplitudu titranja najviše utječu članovi e^{{\text{R}e}\lambda_{1} t} i e^{{\text{R}e}\lambda_{2} t}. Zbog poznatog svojstva eksponencijalne funkcije da za a\le b vrijedi e^{at}\le e^{bt}, za svaki t\ge 0, to ima smisla postaviti kriterij na način da se minimiziraju {\text{R}e}\lambda_{1} i {\text{R}e}\lambda_{2}, odnosno da se minimizira veći od njih, a to je upravo ono što daje kriterij spektralne apscise. Dobru vizualizaciju gore navedenog daje i Slika 1 gdje možemo vidjeti da je u slučaju kritičnog prigušenja sustav najbrže umiren.

Pogledajmo sada koliko bi iznosilo optimalno rješenje koristeći kriterij minimizacije ukupne energije sustava. U tom slučaju potrebno je minimizirati \mathrm{trace}{\textbf{X}} pri čemu je \textbf{X} rješenje matrične jednadžbe (17) gdje je matrica \textbf{A} dana u (19).

Ljapunovljeva jednadžba s nepoznatom matricom \textbf{X} reda n može se zapisati kao sustav n^{2} linearnih jednadžbi sa n^{2} nepoznanica. U slučaju harmonijskog oscilatora nepoznata matrica je drugog reda, tj. \textbf{X}=\begin{bmatrix}{x}_{11}&{x}_{12}\\\ x_{21}& x_{22} \end{bmatrix}. Tada direktnim množenjem matrica u Ljapunovljevoj jednadžbi (za \textbf{A} kao u (19)) te izjednačavanjem komponenti s lijeve i desne strane, dobit ćemo sustav 4 jednadžbe s 4 nepoznanice: Budući da se radi o strukturiranom sustavu jednadžbi, lako se može izračunati da je rješenje x_{11} = 1/\bar{c } + \bar{c} /(2 \omega_{0}^{2}), x_{21}=x_{12} =-1/(2 \omega_{0}), x_{22} = 1/{\bar{c} }. Sada, koristeći \bar{c}=c/m možemo odrediti funkciju koju je potrebno minimizirati Budući da se radi o glatkoj funkciji jedne varijable, standardnim postupkom minimizacije iz dobivamo stacionarnu točku c_{opt}=2\sqrt{\omega_{0}^{2} m^{2}}. Koristeći \omega_{0}^{2}=k/m slijedi c_{opt}=2\sqrt{km}, što se, očekivano, podudara s kritičnim prigušenjem iz poglavlja 2.1. Uočimo i da je funkcija c \mapsto \mathrm{trace} (\textbf{X}(c)) strogo padajuća (derivacija joj je negativna) na \langle 0, c_{opt}\rangle te strogo rastuća (derivacija joj je pozitivna) na \langle c_{opt}, +\infty\rangle, pa možemo zaključiti da je dobiveni c_{opt} točka globalnog minimuma.

Primjetimo da se dobivena optimalna prigušenja za kriterij minimizacije ukupne energije sustava i kriterij spektralne apscise podudaraju: c_{opt}=2\sqrt{km}. Nadalje, ako bismo izračunali optimalni minimum po svim prigušenjima koji je dan formulom (18) dobili bismo također c_{opt}=2\sqrt{km}. Međutim, važno je istaknuti da to općenito nije slučaj. Naime, već za slučaj dvije mase globalni minimum dan s (18) se ne postiže, odnosno pomoću prigušivača u našem modelu ne možemo postići kritično prigušenje. U sljedećem poglavlju ćemo vidjeti na primjeru sustava dvije mase i da se optimalno prigušenje dobiveno minimizacijom ukupne energije sustava općenito ne podudara s optimalnim prigušenjem koji daje kriterij spektralne apscise. Isti se fenomen može primijetiti i kod općenitih titrajnih sustava.

Problem minimizacije funkcije t(\textbf{C}):=\mathrm{trace} \textbf{X(C)} općenito nije jednostavan minimizacijski problem, te često vodi na nekonveksni optimizacijski problem. Općenito, prilikom optimizacijskog postupka potrebno je riješiti velik broj Ljapunovljevih jednadžbi sa matricama velikih dimenzija što je vremenski i numerički vrlo zahtjevno. Rješavanje Ljapunovljeve jednadžbe jedno je od važnih tema u području numeričke linearne algebre gdje se posebna pozornost pridaje što točnijem efikasnom rješavanju te jednadžbe (za neke rezultate vidi [8, 2, 3]). Zbog spomenute složenosti problema, nećemo ulaziti u detaljne dokaze, ali ćemo ilustrirati dio osnovnih rezultata.

Uočimo da bi u slučaju titranja dvije mase matrice koje se pojavljuju u Ljapunovljevoj jednadžbi bile reda 4, što bi značilo da trebamo riješiti 16 jednadžbi sa 16 nepoznanica kako bismo odredili \mathrm{trace} \textbf{X}, pa stoga sustav jednadžbi nećemo precizno zapisivati. Međutim, istaknimo da se, u slučaju dvije mase s jednim prigušivačem c, može pokazati da {\mathrm{trace}}\textbf{X}(c) ima oblik (vidi npr. [9]) {\mathrm{trace}}\textbf{X}(c)=\frac{A}{c}+ B\,c, gdje su A i B konstante dane u terminima početnih parametara našeg sustava. Uočite da se izgled funkcije podudara sa funkcijom dobivenom u (??). Stoga, potpuno analogno kao u prošlom poglavlju može se pokazati da je optimalno prigušenje c_{opt} dano je formulom c_{opt}= \sqrt{A/B}.

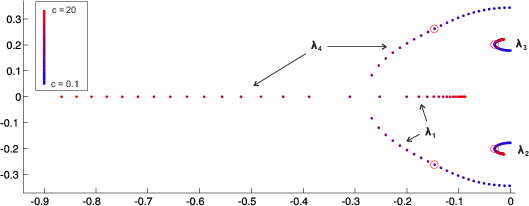
Što se tiče kriterija spektralne apscise, na primjeru ćemo skicirati koliko iznosi optimalno prigušenje te ćemo ga usporediti s optimalnim prigušenjem u slučaju kriterija minimizacije ukupne energije sustava. U tu svhu promotrimo problem titranja dviju masa koji je dan na Slici 4 za sljedeće parametre sustava m_{1}=20, \, m_{2}=40, k_{1}=k_{2}=k_{3}=1, dok vrijednost parametra c varira od 0.1 do 20.

Slika 6 prikazuje kretanje svojstvenih vrijednosti matrice \textbf{A} pri čemu se parametar prigušenja mijenja od malog prigušenja 0.1 pa do velikog prigušenja koji iznosi 20. Analogno kao na Slici 5, kretanje je ilustrirano promjenom boje svojstvenih vrijednosti tako da su svojstvene vrijednosti za prigušenje 0.1 obojane sa plavom bojom, a kako parametar prigušenja raste prema broju 20 tako se boja mijenja prema crvenoj. Sa slike možemo primijetiti da će optimalan c prema kriteriju spektralne apscise biti upravo kada su svojstvene vrijednosti najviše lijevo, što odgovara onom prametru c kada smo dobili svojstvene vrijednosti na slici označene crvenim krugom. Kritično prigušenje postiglo bi se u slučaju kada su sve svojstvene vrijednosti realne, a već sa slike je očito da se to ne može dogoditi.

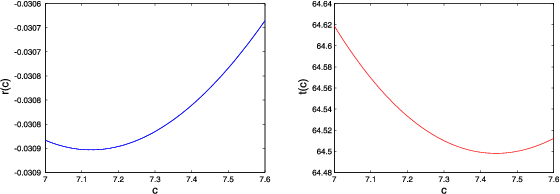
Pokažimo na kraju da optimalna prigušenja za kriterij spektralne apscise i kriterij minimizacije ukupne energije sustava nisu jednaka. Prisjetimo se da optimalna prigušenja odgovaraju minimumima funkcija r(c):= \max_{k} \mathrm{Re} \lambda_{k} za kriterij spektralne apscise, odnosno t(c):=\mathrm{trace}{\textbf{X}(c)}, za kriterij minimizacije ukupne energije sustava. Grafovi tih funkcija (za sustav dvije mase s parametrima m_{1}=20, \, m_{2}=40, k_{1}=k_{2}=k_{3}=1, kao i prije) prikazani su na slici 7.

Iz Slike 7 se jasno vidi da im minimumi nisu isti, odnosno optimalna prigušenja za ova dva kriterija nisu ista. Preciznije, optimalno prigušenje za kriterij spektralne apscise iznosi 7.125, dok za kriterij minimizacije ukupne energije iznosi 7.442. Prisjetimo se da su kod harmonijskog oscilatora optimalna prigušenja bila jednaka, ali kao što je ovdje ilustrirano, to općenito nije slučaj.

U ovom poglavlju su ilustrirane sličnosti, ali i bitne razlike između problema optimalnog prigušenja kod titranja harmonijskog oscilatora i problema titranja dvije mase. Slični fenomeni se pojavljuju i kod titranja složenijih mehaničkih sustava, koji se često mogu diskretizirati i zapisati sustavom (6), ali sa matricama sustava puno veće dimenzije. Tada složenost problema znatno raste, a za određivanje optimalnog prigušenja korisno je i razumijevanje jednostavnijih problema poput onih prikazanih u ovom radu.

U kontekstu optimizacije prigušivača napomenimo da se možemo pitati gdje postaviti prigušivač tako da je sustav optimalno prigušen (u literaturi to zovemo optimizacija položaja prigušivača). U našem slučaju dvije mase, to znači treba li prigušivač postaviti na prvu ili drugu masu. Općenito optimizacija prigušivača (optimizacija položaja i njihovih optimalnih viskoznosti) rezultira nekonveksnim optimizacijskim problemom pri čemu se efikasni optimizacijski algoritam još uvijek traži. Zbog kompleksnosti optimizacijskog problema, obično se pri određivanju optimalnog prigušenja koriste aproksimacijske tehnike (npr. vidi [3, 2]).

Neki složeniji poznati primjeri vibracija građevinskih objekata navedeni su u sljedećem poglavlju.




Do sada smo promatrali optimalno prigušenje slobodnih oscilacija harmonijskog oscilatora i sustava dvije mase. U ovome poglavlju ćemo po prvi puta promatrati sustav na koji dodatno djeluje neka vanjska sila, odnosno promatrat ćemo prisilne oscilacije harmonijskog oscilatora, s posebnim naglaskom na pojavi rezonancije. Složeniji problem prisilnih oscilacija sustava dvije mase ovdje nećemo promatrati.

Preciznije, pretpostavimo da na harmonijski oscilator iz drugog poglavlja djeluje periodična sila oblika f(t)=F\cos (\omega t), za neke F,\omega \in {\textbf{R}}^{+}. Da bi pronašli funkciju pomaka x sada je potrebno još pronaći i partikularno rješenje x_{p} jednadžbe (2). Za ovakav oblik funkcije smetnje f to se može napraviti tzv. metodom neodređenih koeficijenata, koja se sastoji u tome da partikularno rješenje pokušamo pronaći u obliku pri čemu su A_{1} i A_{2} nepoznate konstante. Uvrštavanjem ovakvog x_{p} i njegovih derivacija u (2) lako se izračunaju A_{1} i A_{2}, te se tako dobije formula za rješenjenje.

Pogledajmo najprije što se događa u sustavu bez prigušenja (c=0): ukoliko je \omega\not=\omega_{0} dobije se \displaystyle\ A_{1}=\frac{F}{m(\omega_{0}^{2}- \omega^{2})}, A_{2}=0, pa je opće rješenje jednadžbe (2) jednako pri čemu A i \varphi određujemo iz početnih uvjeta, kao i prije. Uočimo da je ovdje gibanje opisano kao zbroj (superpozicija) dvaju harmonijskih gibanja s periodima \displaystyle\ T_{1}=\frac{2\pi}{\omega_{0}} i \displaystyle\ T_{2}=\frac{2\pi}{\omega}, te pripadnim amplitudama A i \displaystyle\ \frac{F}{m(\omega_{0}^{2}- \omega^{2})}. Primjetimo i da amplituda \displaystyle\ \frac{F}{(\omega_{0}^{2}- \omega^{2})} ovisi o vanjskoj sili te da može biti velika u dva slučaja: ukoliko je amplituda vanjske sile F velika, te ukoliko je \omega približno jednak \omega_{0}. U graničnom slučaju, kada je \omega_{0}=\omega, tj. kada je vlastita frekvencija sustava jednaka frekvenciji vanjske sile, dolazi do pojave poznate pod nazivom rezonancija. 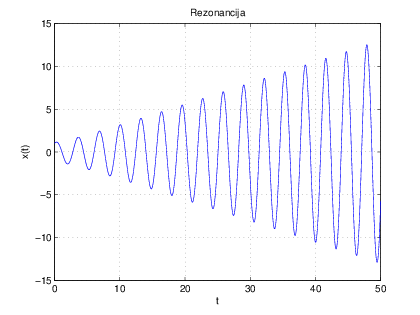Tada partikularno rješenje ne možemo pronaći u obliku (21), nego ga tražimo kao Analogno kao i prije se izračuna A_{1}=0 i A_{2}=\frac{F}{2m\omega}, pa je pomak dan s pri čemu se A i \varphi izračunaju iz početnih uvjeta. I ovdje je pomak superpozicija dvaju gibanja, od kojeg je prvo harmonijsko, dok se kod drugog amplituda linearno povećava s vremenom. Stoga će za dovoljno veliki t amplituda postati prevelika, te će doći do rušenja sustava. Slika 8 prikazuje primjer prisilne vibracije pri pojavi rezonancije.

Rezonancija je jedan od uzroka oštećivanja raznih mehaničkih sustava, a neki poznatiji primjeri rušenja građevinskih konstrukcija kao posljedica rezonancije dani su na kraju ovog poglavlja.

Kako bismo spriječili neželjene posljedice rezonancije, u sustav na koji djeluje vanjska sila f možemo dodati prigušivače. Promotrimo sada naš sustav s vanjskom silom f(t)=F\cos (\omega t), s tim da sada u sustavu imamo prigušenje c\gt 0. Tada je on opisan nehomogenom diferencijalnom jednadžbom Vidjeli smo da izgled rješenja ovisi o nultočkama pripadne karakteristične jednadžbe (slučajevi A,B,C iz poglavlja 2.1). U svakom od tih slučajeva partikularno rješenje možemo pronaći, kao i kod neprigušenih prisilnih vibracija, u obliku I ovaj put nepoznate konstante A_{1} i A_{2} dobivamo deriviranjem i uvrštavanjem u (22), s tim da ovaj put dobivamo nešto kompliciranije izraze: Prema tome, partikularno rješenje je oblika gdje je Sada je funkcija pomaka (opće rješenje jednadžbe (22)) superpozicija prigušenih slobodnih vibracija x_{h} i vibracija x_{p} koje uzrokuje vanjska sila: Pri tome x_{h} ovisi o veličini prigušenja c, pa tako možemo imati malo, veliko ili kritično prigušenje. U svakome od ta tri slučaja smo vidjeli da pomak x_{h}(t) teži nuli kada t \to \infty i on predstavlja tzv. prijelazno rješenje. Drugi dio, x_{p}, je periodična funkcija s periodom \displaystyle\ T=\frac{2 \pi}{\omega} i ne ovisi o početnim uvjetima, već samo o vanjskoj sili. Primjer takvog ponašanja sustava dan je na Slici 9.

Uočimo da ukoliko je \bar{c} dovoljno malen i \omega \approx \omega_{0}, amplituda \widetilde{A} može biti vrlo velika, pa i u ovom slučaju može doći do rezonancije. Stoga se prirodno postavlja pitanje optimalnog prigušenja za prisilne oscilacije. Međutim, to je još složeniji problem od prigušenja slobodnih oscilacija i prelazi okvire ovoga rada.

Na kraju, da bismo još jednom istaknuli važnost problema neželjenih vibracija, navodimo nekoliko primjera vibriranja građevina.

Tacoma Bridge

U srpnju 1940. godine bio je završen i otvoren most u Washingtonu poznat pod nazivom Tacoma Narrows Bridge. Bio je to jedan od najvećih visećih mostova tog vremena. Osiguravala su ga užad koja su jednim krajem bila pričvršćena za tlo, a drugim za dijelove mosta koji su se najviše micali. Od prvoga dana most je počeo vertikalno oscilirati. Nakon samo tri mjeseca užad namijenjena stabiliziranju mosta su popucala tijekom oluje. Iako su zamijenjena, most je sve više oscilirao prilikom jačih vjetrova. U studenome iste godine, uz brzinu vjetra od oko 65 km/h,u jednom trenutku jedan kraj ceste bio je 8 metara viši od drugog, a u drugom pak 8 metara niži od drugog. Ubrzo nakon toga most se raspao. Uzrok ove katastrofe jest upravo rezonancija: uslijed izjednačavanja frekvencije mosta i frekvencije vjetra amplituda titranja mosta je postala prevelika, te se on srušio.

Kasnije je most je obnovljen, no sada ima nosače koji su 10 metara duboko u tlu, a ne 2.4 metra kao kod prvotnog mosta i ima četiri, a ne dvije trake. Masa novog mosta je duplo veća od starog, i još uvijek je u uporabi ([4, 10]).

Millenium bridge

Milenijski most, poznat kao i Londonski milenijski pješački most je čelični viseći pješački most preko prijeke Temze u Londonu. Otvoren je u lipnju 2000. godine, a dobio je nadimak Wobbly Bridge (Nesiguran most) nakon što su pješaci osjetili neočekivano ljuljanje u prva dva dana nakon otvorenja. Most je tada zatvoren, te se nije otvarao iduće dvije godine, sve dok ljuljanja nisu posva uklonjena. Što je bio uzrok gibanja mosta? Na dan otvaranja most je prešlo 90 000 ljudi, čija je kretnja uzrokovala male bočne oscilacije mosta. Ne samo Milenijski most, nego i bilo koji most bočne frekvencije manje od 1.3 Hz i dovoljno male mase može svjedočiti istom problemu. Što je veći broj ljudi na mostu, to je i veća amplituda vibracija. Nakon opsežne analize inženjeri su uklonili problem Milenijskog mosta ugradnjom 37 viskoznih prigušivača koji kontroliraju horizontalno gibanje, te 52 masovna prigušivača koji kontroliraju vertikalno gibanje mosta. Nakon provedenih testiranja, most je otvoren, te otada nije bilo nikakvih značajnih vibracija mosta ([11]).

Viseći most u Broughtonu

Pojava rezonancije je odgovorna i za urušavanje visećeg mosta u Broughtonu pored Manchestera, 1831. godine. Ovo se dogodilo kada je kolona vojnika marširala preko mosta, stvarajući pri tome periodičnu silu dosta velike amplitude. Frekvencija te sile bila je jednaka prirodnoj frekvenciji mosta. Tako su bile pobuđene vrlo velike vibracije i most se raspao. Upravo zbog ovoga razloga dana je naredba vojnicima da se marš prekida prilikom prelaska preko mosta ([4]).

Most Franje Tuđmana

Most Franje Tuđmana u Dubrovniku sagrađen je 2001. godine. Asimetrična konstrukcija ima 143 metra visok toranj na koji je sa svake strane pričvršćeno je 19 čeličnih konopa od kojih najveći ima duljinu 220 metara. U ožujku 2005. i 2006. godine snježne oluje su uzrokovale ekstremne vibracije tih konopa, od kojih je najduži vibrirao amplitudom do 2 metra. Stoga su stručnjaci odlučili postaviti vibracijske prigušivače. Postavljeni su vertikalno između ceste i konopa, te pričvršćeni za konop otprilike 3.5 metra iznad ceste. Rezultati su pokazali da su vibracije smanjene za faktor 10. Iskustvo pokazuje da bi ovi prigušivači trebali osigurati da se u budućnosti, čak i pod uvjetima snažnog vjetra, konoplje mosta zanjiše s malom amplitudom koja nije presudna građevinskoj sigurnosti. Izračuni pokazuju da amplituda vibriranja konoplja u najgorem slučaju neće prelaziti 15-20 cm ([12]).

Burj al Dubai i Taipei

Burj al Dubai, poznat i kao Burj Khalifa, najviša je svjetska građevina, visine 828 metara, sa 206 katova. Posebno je dizajniran kako bi se smanjio utjecaj snage vjetra na toranj. Naime, temelji Bujr al Dubai-a postavljeni su u obliku slova "Y", a zgrada se diže u nebo u nekoliko odvojenih stupova koji se uzdižu oko centralnog tornja. Taj dizajn odmiče vjetar od građ evine i sprječava ga u stvaranju vrtloga zračnih struja koje bi uzrokovale ljuljanje zgrade. Usprkos ovome strateškom dizajnu, Burj Khalifa se njiše pri vrhu amplitudom 2 metra. Poput mnogih nebodera, Bjur Khalifa za smanjivanje utjecaja vjetra koristi i tzv. strateške masivne prigušivače. To su ogromna njihala čiji oblik i veličina ovise o masi i visini svakog odvojenog tornja. Kako vjetar puše i gura zgradu u jednom smjeru, tako prigušivač klizi u suprotnom smjeru, smanjujući tako ljuljanje zgrade.
Ovakav prigušivač ima i druga po redu najviša svjetska građevina, neboder Taipei 101 u Tajvanu. Unutar nebodera, između 88. i 92. kata smješteno je ogromno njihalo (prigušivač) koje vodi tihu bitku s velikim olujama i tajfunima. Metalna kugla, težine 730 tona, blago se njiše naprijed-nazad, te tako štiti neboder od sile vjetra i osigurava udobnost njegovim stanarima ([13, 14]).

Katedrala sv. Petra u Beauvais-u

Katedrala sv. Petra u Beauvais-u u Francuskoj visoka je 153 metra i jedno je od najdragocjenijih postignuća gotičke arhitekture. Sa željom da se sagradi najviša katedrala u 13. stoljeću, graditelji su prešli granice tadašnje tehnologije. Iako je katedrala bila tada najviša na svijetu, imala je relativno tanke potporne stupove kako bi što više svjetlosti moglo ući u nju. 12 godina nakon što je sagrađena, kor katedrale se urušio, zajedno s nekoliko gornjih potpornja. Za ovu katastrofu odgovorna je rezonancija koja je nastala pod utjecajem snažnih vjetrova koji su došli s engleskog kanala. Kor je obnovljen, a dodani su i masivni potpornji kako bi stabilizirali sjevernu stranu katedrale. Iako je broj potpornja udvostručen, i danas katedrali prijete olujni udari vjetrova koji uzrokuju njihovo vibriranje i slabljenje krovnih greda. Znanstvenici diljem svijeta proučavaju katedralu i pokušavaju naći rješenje kako bi spriječili novu katastrofu ([15, 16]).





 

Tijela koja rotiraju nalazimo u mnogim mehaničkim uređajima, pa i onima kojima se i sami služimo. Ovdje ćemo se posebno baviti izduženim tijelima koja se rotiraju oko svoje „izdužene” osi. Primjer su svrdla raznih bušilica (klasične ručne ili one za bušenja u geologiji, vađenju nafte), razne osovine (vratila) za prijenos snage, kao kod automobila, brodova ili u primjeru rotora turbina elektrana.

Kod svih ovih primjera mehaničkih sustava tijelo rotira oko svoje osi. Potencijalni problemi dolaze zbog utjecaja centrifugalne sile koja teži izbaciti sustav iz pravilne vrtnje.
Tipično, to se događa za dovoljno velike brzine vrtnje. Posljedice su velike vibracije koje mogu uništiti čitav sustav. Jednom kad izgradimo konkretan sustav, relativno ga je lako eksperimentalno testirati i provjeriti radi li on korektno u radnim uvjetima. No, ako smo ga izgradili „na slijepo”, velike su šanse da nije racionalno izgrađen (ili je predimenzioniran ili iskazuje određene nedostatke, primjerice nestabilnost). Stoga je od interesa modelirati konkretni mehanički sustav da bismo ga lakše projektirali. U našem konkretnom slučaju poželjno je unaprijed znati koje su to brzine koje će producirati nestabilnu vrtnju.

U ovom nam je radu u cilju izložiti čitav proces modeliranja rotirajućih štapova. Počinjemo s opisom teorije i smještanjem problema u okvire te teorije. Zatim tu teoriju primjenjujemo na konkretni problem rotirajućeg štapa. Dobiveni model smještamo u matematički kontekst, te matematički analiziramo problem. Nakon toga određujemo analitička rješenja problema za neke specijalne slučajeve (i jedine kada je to i moguće u našem primjeru), te donosimo numeričke aproksimacije rješenja. Na kraju uspoređujemo dobivene rezultate (analitičke i numeričke) s rezultatima eksperimenta, te time konačno potvrđujemo model.



„Izduženo” tijelo koje se rotira u nastavku nazivamo tanki štap. Tanki štap \Omega \subset \mathbb{R}^{3} opisujemo kao trodimenzionalno tijelo kojem su dvije dimenzije („debljine”) malene u odnosu na treću („duljinu”, L\gt 0):
u inženjerskoj literaturi tipično se pretpostavlja da je debljina / duljina \lt 1/ 30. Malo preciznije, neka je dana familija \lbrace D(x_{3})\subset \mathbb{R}^{2}_{x_{1} x_{2}}: x_{3} \in (0, L)\rbrace. Štap definiramo s Skupove D(x_{3}) zovemo poprečni presjeci štapa u točki x_{3}. Dopuštamo ovisnost o točki poprečnog presjeka jer su nam baš takvi i realni primjeri. Sada tankoću štapa iskazujemo zahtjevom: \mathop{\rm diam}\nolimits{D(x_{3})}\ll L. Specijalno, od interesa će nam biti samo ravni štap. To je onaj kojemu je centralna linija (linija koja prolazi kroz težišta poprečnih presjeka) ravna. Stoga pretpostavljamo da vrijedi Radi jednostavnosti, ovdje dodatno pretpostavljamo da poprečni presjeci zadovoljavaju dodatni uvjet simetrije (zadovoljen je, naprimjer, za kružni i pravokutni poprečni presjek).


Djelujući silom naprimjer na tanki čelični štap, on se deformira. Uklonimo li silu kojom smo djelovali, štap se vraća u nedeformirani (prvobitni) položaj. Tipičan primjer takvog ponašanja je opruga. Tijela koja se pri djelovanju sile deformiraju, a nakon uklanjanja sile vraćaju u prvobitni položaj, nazivamo elastičnim tijelima, a teoriju koja se njima bavi teorijom elastičnosti.

Tanki elastični štap je prema prethodnom opisu trodimenzionalno elastično tijelo. Jednadžbe trodimenzionalne teorije elastičnosti, čak i one linearizirane (pojednostavljene uz pretpostavku neznatne deformacije), komplicirane su. No, u slučaju posebnih geometrija tijela, kao u slučaju štapa, moguće je izvesti jednostavnije modele ponašanja (slično je u primjeru opruge, koja je trodimenzionalno elastično tijelo; njeno je ponašanje vrlo kompleksno za precizan opis, ali znamo da je „osnovno” ponašanje modelirano jednadžbom F=k x; F je sila koju primjenimo na oprugu, x pripadno izduženje (skraćenje) opruge, a k krutost opruge). Geometrijski tanki štap možemo „dobro” opisati njegovom centralnom krivuljom, parametriziranom s (0,0,x_{3}), x_{3}\in (0,L), a „dobro” ovdje znači do na najveći dijametar poprečnih presjeka. Pokazuje se da se i deformacija tankog elastičnog štapa može opisati deformacijom centralne krivulje štapa, parametriziranom s \mathbf{\Psi}(x_{3}) \in \mathbb{R}^{3}, x_{3}\in (0,L).

I opet je pogreška takvog modela, među ostalim, vezana za najveći dijametar poprečnih presjeka. Izvod takvog modela daje i malo više. Naime, pokazuje se da se deformacija tankog elastičnog štapa može opisati kroz deformaciju centralne linije štapa, te kroz infinitezimalnu krutu deformaciju poprečnih presjeka (infinitezimalna kruta deformacija je translacija i rotacija, s tim da je rotacija aproksimirana sumom matrica I+A, gdje je I identiteta, a A antisimetrična matrica. Naime, može se pokazati da je svaka rotacija R=e^{A}, za neku antisimetričnu matricu, pa je I+A zapravo Taylorov polinom 1. stupnja za R).
Takva deformacija \mathbf{\Psi}(x), x \in \Omega s pomoću pomaka \mathbf{U}(x) = \mathbf{\Psi}(x) - x može se zapisati formulama Ovdje je \mathbf{u}(x_{3})=(u_{1}(x_{3}),u_{2}(x_{3}),u_{3}(x_{3})) pomak točke (0,0,x_{3}) centralne linije štapa, u'_{1}(x_{3}) opisuje kut zakreta poprečnog presjeka na mjestu x_{3} oko osi \mathbf{e}_{2}, u'_{2}(x_{3}) opisuje kut zakreta poprečnog presjeka na mjestu x_{3} oko osi \mathbf{e}_{1}, a \omega(x_{3}) opisuje kut zakreta poprečnog presjeka na mjestu x_{3} oko osi \mathbf{e}_{3} (torziju). Ovakav oblik pomaka naziva se Bernoulli–Navierov (ili Kirchhoff–Love) pomak.

Budući da ćemo promatrati stabilnost rotirajućeg štapa u odnosu na transverzalni pomak (okomit na centralnu liniju), u nastavku pišemo samo jednadžbe koje zadovoljavaju transverzalni pomaci (u_{1},u_{2}). To su obične diferencijalne jednadžbe četvrtog reda: (vidi npr. [4], [6]). Ovdje su (f_{1}, f_{2}) i (m_{1}, m_{2}), redom, linijska gustoća transverzalne sile i momenta (to znači da je \int_{a}^{b} f_{1} dx_{3} komponenta ukupne sile u smjeru \mathbf{e}_{1}=(1,0,0) na komad štapa \lbrace x\in \mathbb{R}^{3}: (x_{1},x_{2} \in D(x_{3})), x_{3} \in [a,b]\rbrace). E\gt 0 je Youngov modul elastičnosti materijala (opisuje svojstvo materijala od kojeg je štap napravljen), a I_{\alpha} (x_{3}), \alpha=1, 2, su momenti inercije poprečnog presjeka D(x_{3}) – opisuju geometriju poprečnog presjeka štapa: Funkcija \sigma(x_{3}) je longitudinalna napetost štapa (npr. u slučaju bušilice sila kojom je pritišćemo primjerice na zid). Strogi izvod ovog modela može se naći u [6] i [7].


U nastavku ćemo iskoristiti model (3) za štap koji se rotira konstantnom kutnom brzinom \gamma, te na njega ne djeluju druge sile osim centrifugalne. Očito je riječ o dinamičkom problemu, što znači da bismo se morali koristiti jednadžbama gibanja, a ne ravnoteže. No, ako odaberemo koordinatni sustav vezan za štap koji se rotira, u tom koordinatnom sustavu štap miruje. U modelu (3) transverzalni pomak uzrokovan je centrifugalnom silom i njome uzrokovanim momentom. Stoga ih, u koordinatnom sustavu u kojem štap miruje, računamo po formulama gdje je \mathbf{e}_{3} =(0, 0, 1); \varrho \in \mathbb{R}^{+} je linijska gustoća mase (\rho d je masa komada štapa duljine d), a \times označava vektorski produkt (ovo su uobičajene formule za centrifugalnu silu \mathbf{\gamma} \times (\mathbf{\gamma} \times \mathbf{r}), gdje je \mathbf{\gamma} vektor kutne brzine, a \mathbf{r} radij vektor mase; jedini je dodatak integral po svim točkama tijela jer nije riječ o masi u točki).

Koristeći Bernoulli-Navierov oblik pomaka (2), u stanju smo prikazati silu i moment s pomoću transverzalnog pomaka centralne linije: ovdje je S(x_{3}) = | D(x_{3})| površina poprečnog presjeka na mjestu x_{3}.

Uvrštavanjem ovih sila i momenata u jednadžbe modela (3) dobivamo dvije jednadžbe gdje smo uveli konstantu Ovo su jednadžbe za transverzalni pomak u oba transverzalna smjera. S obzirom na to da su jednadžbe iste, u nastavku pišemo samo jednu U slučaju kada su oba kraja štapa ukliještena (nije dopušten progib ni rotacija poprečnog presjeka na rubu), uz ovu jednadžbu pridružujemo i rubne uvjete

U slučaju kad su oba kraja učvršćena šarnirom (nije dopušten progib, dok je rotacija slobodna na krajevima), rubni uvjeti su

Zadaća za pomak štapa pri rotaciji sada glasi: naći funkciju u koja zadovoljava jednadžbu (7) te jedan od rubnih uvjeta (8) ili (9), ovisno o problemu koji promatramo (čak možemo i kombinirati različite rubne uvjete na oba kraja). Jasno je da za svaki \lambda \in \mathbb{R} jedno rješenje ovih zadaća funkcija u=0. Pitanje je postoje li možda i neka druga rješenja za određene \lambda (možda ne za sve). Stoga je i \lambda nepoznanica u problemu i on sada glasi: naći sve \lambda \in \mathbb{R} i funkcije u koje nisu nul-funkcije za koje vrijedi ili u slučaju drugih rubnih uvjeta Zadaće ovog tipa nazivaju se svojstvene zadaće (ili spektralne zadaće), a ovo su primjeri svojstvenih zadaća za linearni diferencijalni operator (4. reda). Rješenja su zapravo uređeni parovi (\lambda, u_{\lambda}) realnog broja \lambda i nenul-funkcije u_{\lambda} koja rješava rubnu zadaću za diferencijalnu jednadžbu za dani \lambda. \lambda se naziva svojstvena vrijednost, a pripadni u_{\lambda} svojstveni vektor ili svojstvena funkcija. Za primijetiti je da takav u_{\lambda} nije jedinstven jer je i svaka funkcija oblika c u_{\lambda}, za c\in \mathbb{R} također svojstvena funkcija.

Najjednostavniji primjer svojstvenih zadaća su svojstvene zadaće za linearne operatore na konačnodimenzionalnim vektorskim prostorima koje se reduciraju na matrične svojstvene zadaće (vidi Linearnu algebru).

Matematička teorija ovakvih svojstvenih zadaća bazirana je na spektralnoj teoriji kompaktnih linearnih operatora [3]. Osnovni je rezultat za našu svojstvenu zadaću da je spektar (skup svih svojstvenih vrijednosti) prebrojiv (ima članova koliko ima i prirodnih brojeva), te da nema konačnog gomilišta. Ovo zajedno daje da je spektar diskretan. Spektar u nastavku označavamo s \Lambda.

U ovom problemu nenul–rješenja dolaze iz dvaju izvora: rotacije štapa te longitudinalne sile koja djeluje na štap. Naprimjer, pretpostavimo da se štap ne rotira; uzmemo li dovoljno tanki čelični štap i pritisnemo li ga duž osi štapa, doći će do transverzalnog progiba ako smo primijenili dovoljno veliku silu.

Taj slučaj nestabilnosti bez vrtnje (Eulerova nestabilnost, vidi [4]) ovdje isključujemo zahtjevom (vidi [1]) pri čemu je
Zbog definicije broja \lambda u (6) i našeg problema jasno je da su nam od interesa samo \lambda \gt 0. Stoga se ograničavamo na promatranje skupa \Lambda \cap \mathbb{R}^{+}. Označimo s tim da definiramo \lambda_{0} = +\infty ako je skup \Lambda \cap \mathbb{R}^{+} prazan. Sada je štap stabilan za kutne brzine rotacije \gamma koje zadovoljavaju Kutnu brzinu vrtnje \gamma_{\scriptsize{\mbox{kritična}}} zovemo kritična brzina. Osim u jednom, dva slučaja kritičnu brzinu nije moguće točno izračunati. Ostaju nam dvije mogućnosti aproksimacije kritične brzine. Jedna je bazirana na analitičkoj ocjeni kritične brzine odozdo i izvedena je u [1]. Druga je numerička aproksimacija bazirana na metodi konačnih elemenata (Finite Element Method, FEM) i prikazana je u [5]. Analitičku ocjenu odozdo donosimo sljedećem teoremu


Ovaj rezultat zapravo kaže: ako je štap dovoljno „debeo” nema nestabilnosti; inače, nestabilnost je moguća samo za brzine rotacije veće od \overline{\gamma}.


Ovdje donosimo dva primjera. U prvom primjeru (vjerojatno je i jedini takav) znamo izračunati analitička rješenja našeg problema. U drugom primjeru svedemo određivanje svojstvenih vrijednosti na problem nultočaka nelinearne funkcije. U oba slučaja riječ je o štapu konstantnog poprečnog presjeka te konstantne uzdužne sile \sigma. Za sve druge slučajeve zadaću moramo numerički rješavati.




Model rotirajućeg štapa nije moguće analitički riješiti čim neki od koeficijenata nije konstantan (npr. poprečni presjek nije konstantnog radijusa duž štapa). U svim tim slučajevima problem rješavamo numerički, metodom konačnih elemenata, vidi [5].






Da bismo neki model upotrijebili u praksi, najčešće je nužna verifikacija modela s pomoću eksperimenta. Postavljanje i vođenje eksperimenta iznimno je zahtjevan zadatak te traži puno inženjerskog znanja i iskustva. Fizikalni model izrađen je i ispitivan na Katedri za turbostrojeve Fakulteta strojarstva i brodogradnje Sveučilišta u Zagrebu. Eksperiment su organizirali i vodili prof. dr. sc. Branimir Matijašević i prof. dr. sc. Zvonimir Guzović.
Osnovni podaci eksperimenta su sljedeći:

\bullet	duljina štapa: L=0.835m
\bullet	promjer štapa: 2R=0.01m
\bullet	uzdužna napetost: \sigma = 0N
\bullet	materijal štapa: čelik
\bullet	Youngov modul elastičnosti: E=2.1 \, 10^{11}Pa
\bullet	gustoća: \varrho = 7800 \frac{\text{kg}}{\text{m}^{3}}

Obavljena su dva eksperimenta — jedan za ukliještene krajeve i jedan za krajeve učvršćene šarnirom. Za određivanje kritične brzine korišten je stroboskop (Slika 23),
dok je za rotaciju štapa korišten elektromotor (Slika 24).
Ograničenja korištenih uređaja omogućila su određivanje samo prvih dviju kritičnih brzina.


U slučaju ovih rubnih uvjeta, matematički model te eksperiment daju rezultate u Tablici 7.
Iz rezultata vidimo da je razlika za prvu kritičnu brzinu ispod 1%, a za drugu ispod 3%.


U slučaju ovih rubnih uvjeta, matematički model te eksperiment daju rezultate u Tablici 8.
Rezultati eksperimenta jako odudaraju od onih dobivenih iz modela. Naravno, u ovom slučaju delikatna je implementacija rubnih uvjeta. Za primijetiti je da je 1. kritična brzina zapravo vrlo bliska onoj iz 1. eksperimenta.