Bertrandov paradoks
Bertrandov paradoks
Bertrandov paradoks je problem iz vjerojatnosti, koji je francuski matematičar Joseph Bertrand (1822. – 1900.) predstavio u svom djelu Calcul des probabilités (1888.) kao primjer koji pokazuje da vjerojatnosti ne moraju biti dobro određene ako metoda kojom generiramo slučajnu varijablu nije jasno zadana.
Paradoks glasi:
Kolika je vjerojatnost da duljina slučajno odabrane tetive kruga bude veća od stranice krugu upisanog jednakostraničnog trokuta?
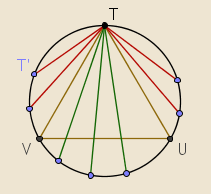
Prvo rješenje - slučajne krajnje točke.
Izaberemo točku T na kružnici i upišemo u krug jednakostraničan trokut \Delta TUV s vrhom u T. Nakon toga izaberemo drugu točku T' na kružnici i povučemo tetivu \overline{TT'}. Za točke T' takve da \overline{TT'} siječe stranicu \overline{UV} tetiva je dulja od stranice trokuta. Budući da je duljina luka UV jednaka jednoj trećini opsega kružnice, vjerojatnost da je slučajno odabrana tetiva dulja od stranice upisanog trokuta je \frac{1}{3}.
Drugo rješenje - slučajna udaljenost od središta.
Izaberemo neki radijus i rotiramo trokut tako da je jedna stranica okomita na radijus. Izaberemo točku na radijusu i konstruiramo tetivu čije je polovište odabrana točka. Duljina tetive veća ja od duljine stranice trokuta ako je udaljenost tetive od središta manja od polovice radijusa, pa je tražena vjerojatnost \frac{1}{2}.
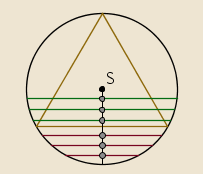
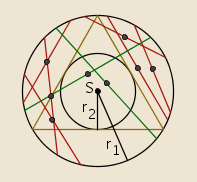
Treće rješenje - slučajno odabrano polovište tetive.
Izaberemo bilo koju točku unutar kruga kao polovište tetive. Ako točka pada unutar trokutu upisane kružnice, duljina tetive je dulja od stranice trokuta. Budući da je radijus upisane kružnice r_2 jednak polovici radijusa opisane kružnice, r_1 , površina upisane kružnice, P=r_2^2\cdot\pi, jednaka je četvrtini površine zadanog kruga. Dakle, tražena vjerojatnost je \frac{1}{4}.
Iako smo dobili tri različita rezultata, ni u jednom rješenju ne možemo pronaći pogrešku. Također, možemo napraviti tri različita fizička pokusa za svaku od navedenih situacija i potvrditi dobivene rezultate.
- Dva puta zavrtimo kazaljku i označimo točke na kojima se zaustavi.
- Iz daljine bacamo slamke na mali krug.
- Nasumice gađamo krug strelicama i tako odredimo polovišta tetiva.
Ne postoji jedinstvena metoda biranja slučajnih točki, pa ne možemo imati ni jedinstveno rješenje. Problem je u biti potpuno zadan tek kad znamo metodu slučajnog izbora točki i tada ima dobro definirano rješenje.