Braessov paradoks

Braessov paradoks dobio je ime po svom tvorcu - matematičaru Dietrichu Braessu. 1968. godine Braess je predstavio primjer problema stvaranja ekvilibrija koji daje naoko paradoksalan rezultat. Odnosi se na iznenađujuće smanjenje (u smislu pogoršanja) u izvedbi nekih mreža kao rezultat dodavanja kapaciteta. Pojava ovog smanjenja proučavana je kao matematički model ekvilibrijskog toka u cestovnom (željezničkom) prometu, računalnim mrežama, telefonskim mrežama, sustavima za opskrbu vode, električnim krugovima i slično.

Braessov paradoks tvrdi da dodavanje kapaciteta mreži, u slučaju kad krećući entiteti sebično biraju put, u nekim slučajevima smanjuje sveukupnu performansu.

Primjeri iz stvarnog života:

• 1990. godine, 42. ulica u New Yorku bila je zatvorena, no usprkos predviđenog zastoja, promet se poboljšao.
• Nakon što je 1969. u Stuttgartu konstruirana nova cesta, protok prometa pogoršao se i postao je bolji tek nakon što je novoizgrađena cesta bila zatvorena.

Pretpostavimo da 100 automobila putuje iz A u D, te da mogu voziti putem ABD ili putem ACD, kao na Sl. 1. Cijena svakog puta je vrijeme potrebno za prijeći put. Trajanje puta od A do B je \frac{x}{100}, gdje je x broj automobila na putu AB. Cijena puta BD je 3, cijena puta AC je isto 3, a cijena puta CD je \frac{x}{100}.

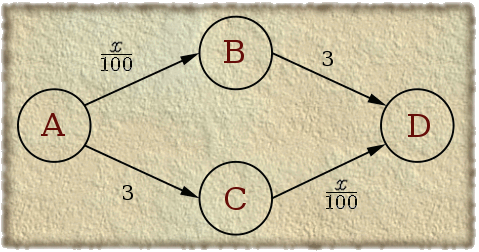Sl. 1. Prometna mreža

Pretpostavimo da će vozači na temelju iskustva izabrati put koji je za njih optimalan. Kad oba puta imaju jednak protok, mreža je u stanju ekvilibrija. Niti jednom vozaču nije u interesu promijeniti put jer bi time sebi povećao trajanje putovanja. U našem primjeru to je slučaj za x = 50. Tada je cijena puta za pojedini automobil jednaka 3.5.

Promotrimo što se dogodi ako izgradimo novu cestu BC cijene 1.7 (sl. 2).

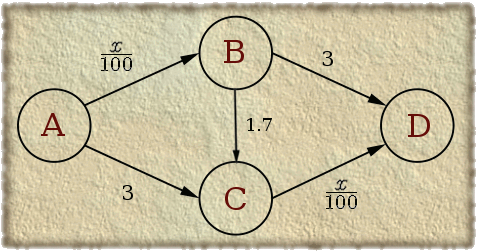Sl. 2. Prometna mreža nakon izgradnje nove ceste

Sad će vozač koji stigne u B nastaviti putem BCD jer je taj put i u najgorem slučaju (za x = 100) brži od BD. Put BCD ima najveću cijenu 2.7.

No, ako svi krenu putem ABCD, vrijeme potrebno za dolazak iz A u D će postati 3.7, što je više nego prije izgradnje nove ceste. Pojedini vozač ni sad nema razloga izabrati drugi put jer bi time povećao trajanje puta.

Vidimo da unatoč tomu što je svaki vozač izabrao najpovoljniji put za sebe, niti jedan od njih ne postiže vrijednost koju bi mogli postići pri optimalnom protoku. Dodavanje ceste postojećoj cestovnoj mreži dovelo je do sporijeg prolaska.

Paradoks se može promatrati kao slučaj Nashova ekvilibrija.
Više o paradoksu može se pročitati na web stranici profesora Braessa.