|
Vlado Halusek, Tibor Rodiger i Marijana Špoljarić |
Ključne riječi: matrice, operacije s matricama, sustavi linearnih jednadžbi, matrični kalkulator
Sažetak
Matrice u visokoškolskoj matematici nezaobilazni su dio sadržaja kojeg studenti moraju savladati. Shvaćanje pojma matrica ne predstavlja velik problem za studente kao ni operacije transponiranja, zbrajanja i oduzimanja. Problemi nastaju kod množenja, traženja inverza i rješavanja sustava linearnih jednadžbi primjenom Gaussove metode transformacija. Matrix Reshish je mrežna stranica koja je prilagođena za korištenje putem mobilnih uređaja, a sadrži matrični kalkulator. Kalkulator je koncipiran tako da daje rješenje postavljenog zadatka korak po korak, što uvelike olakšava studentu uvježbavanje rješavanja zadatka.
1Uvod
U brojnim se slučajevima zbog preglednosti podaci zapisuju u tablicama. Ako se s takvim tablicama mogu izvoditi određene računske operacije, onda se one zovu matricama. Zapisivanje podataka pomoću matrica omogućuje kodiranje različitih oblika njihove povezanosti i potom ispitivanje postoji li među određenim objektima neka od mogućih veza. Matrice se između ostalog koriste za zapisivanje i obradu podataka, za različito modeliranje u ekonomici, u kompjutorskoj grafici itd. [str. 69]- [4].
Linearna algebra pomoću matrica omogućuje:
|
(1) |
sažet način pisanja sustava linearnih jednadžbi, čak i jako velik sustav, |
|
(2) |
traženje rješenja linearnih jednadžbi i provjeru postojanja rješenja računanjem determinante [str. 54]- [3]. |
Matrice se mogu množiti samo ako prva od njih ima toliko stupaca koliko druga ima redaka, pri čemu se kao rezultat dobije matrica koja ima redaka kao i prva, a stupaca kao druga matrica. Dakle, matrica C_{(m,p)} koja je umnožak dviju matrica može se dobiti samo ako te dvije matrice imaju oblik A_{\left(m,n\right)} i B_{(n,p)}, to jest
A_{\left(m,n\right)} \cdot B_{(n,p)} =C_{(m,p)} .
Osnovno pravilo množenja matrica je da na mjesto (i, j) u umnošku matrica dolazi umnožak i-tog retka prve matrice i j-tog stupca druge matrice. Taj umnožak se računa po elementima tako da se pomnoži prvi element i-tog retka s prvim elementom j-tog stupca, drugi element i-tog retka s drugim elementom j-tog stupca itd. Na kraju se vrijednost elementa (i, j) dobije tako da sve te umnoške zbrojimo. To možemo prikazati na sljedeći način:
c_{ij} =\sum _{k=1}^{n}a_{ik} b_{kj} ,i\in \left\lbrace 1,2,3,...,m\right\rbrace ;j\in \left\lbrace 1,2,3,...,n\right\rbrace [str. 199]- [5].
Studenti s lakoćom znaju prepoznati koje matrice mogu množiti, a koje ne. Najčešća greška koju rade kod množenja matrica je da krenu s množenjem i-tog retka prve matrice i j-tog stupca druge matrice za prva dva retka matrice, a zatim nastave množenje tako da stupac množe retkom. Isto tako, često pogriješi kod samog množenja i predznaka umnoška. Kod kvadriranja matrice studenti najčešće svaki element matrice kvadriraju i ne koriste pravilo za umnožak dviju matrica, odnosno
A^{2} =A\cdot A.
Kod traženja inverza matrice najčešće će se koristiti determinantama, a rijetko kada svođenjem na reducirani oblik pomoću elementarnih transformacija:
|
(1) |
dvije jednadžbe zamijene mjesto, |
|
(2) |
jednadžbu sustava množi se s konstantom različitom od nule, |
|
(3) |
jedna jednadžba, pomnožena konstantom, pribroji se drugoj jednadžbi [str. 194]- [1], |
koje se koriste u Gaussovom postupku. Elementarnim transformacijama dolazi se do jedinične matrice s lijeve strane proširene matrice. To zahtijeva kreativnost i predviđanje bar dva koraka unaprijed što će se dogoditi s matricom, a studenti najčešće ne znaju ni kako započeti rješavanje zadatka pogotovo ako su svi elementi u prvom stupcu različiti od jedan.
Kalkulatori koje studenti najčešće imaju omogućavaju rješavanje osnovnih računskih operacija s matricama do reda 3\times 3. I oni daju rješenje postavljenog problema bez postupka kojim se došlo do tog rješenja. Upravo zbog toga studenti kalkulatorima i kontrolom rješenja u zbirkama zadataka mogu pronaći samo točno rješenje, ali ako su pogriješili ne mogu pronaći grešku i najčešće odustaju od potrage za rješenjem. Kako bi studenti savladali ishode učenja o matricama i sustavima linearnih jednadžbi, a time i položili predmet kojeg su slušali, može im pomoći matrični kalkulator na Internet stranici http://matrix.reshish.com/ i http://matrix.reshish.com/.
2Matrix Reshish
Matrix Reshish [9] je mrežna stranica s besplatnim online matričnim kalkulatorom. Algoritam kojeg koristi Matrix Reshish temelji se na Binet-Cauchyevom teoremu i LU rastavu. Zbog toga je numerički stabilan, a složenost mu je \mathcal{O}=n^{3}. Reshish Matrix kalkulator omogućava izračunavanje svih osnovnih matričnih operacija i metoda koje se koriste za rješavanje sustava linearnih jednadžbi (tablica 1).
\eject Tablica 1. Popis metoda i operacija nad matricama koje omogućava Reshish Matrix kalkulator
|
Naziv metode na engleskom jeziku |
Naziv metode na hrvatskom jeziku |
Opis metode/operacije |
|
Gauss-Jordan Elimination |
Gauss-Jordanova eliminacija |
Rješavanje sustava linearnih jednadžbi primjenom Gauss-Jordanove metode eliminacije. Kalkulator rješava jednostavne sustave i neodređene sustave koji imaju beskonačno mnogo rješenja. U slučaju beskonačno mnogo rješenja dobit će se ovisnost jedne varijable o drugoj. Koeficijenti linearnih jednadžbi mogu biti i kompleksni brojevi |
|
Cramer's Rule |
Cramerovo pravilo |
Rješavanje sustava linearnih jednadžbi primjenom Cramerovog pravila. Koeficijenti linearnih jednadžbi mogu biti i kompleksni brojevi. Kalkulator rješava svaku determinantu sustav posebno |
|
Inverse Matrix Method |
Metoda inverza matrica |
Rješavanje sustava linearnih jednadžbi primjenom metode inverzne matrice. Koeficijenti linearnih jednadžbi mogu biti i kompleksni brojevi |
|
Matrix Rank |
Rang matrice |
Izračunavanje ranga matrice |
|
Determinant |
Determinanta |
Izračunavanje determinante matrice |
|
Inverse Matrix |
Inverz matrice |
Izračunavanje inverza matrice Gaussovom metodom eliminacije |
|
Matrix Power |
Kvadriranje matrice |
Izračunavanje kvadrata zadane matrice |
|
Matrix Transpose |
Trensponirana matrica |
Izračunavanje transponirane matrice |
|
Matrix Multiplication |
Množenje matrica |
Izračunavanje umnoška dviju matrica. Matrice mogu biti i jednodimenzionalne (vektor) tako da se može izračunati umnožak vektora, matrice i vektora i obrnuto |
|
Matrix Addition/ Substraction |
Zbrajanje i oduzimanje matrica |
Izračunavanje zbroja i razlike dviju matrica |
Izvor: autori
Matrix Reshish omogućava ne samo rješenje postavljenog problema, nego i detaljan proces rješavanja, korak po korak, u nizu jednostavnih tablica. Ovaj način prikaza rješenja omogućava korištenje ovog alata za učenje i poučavanje. Za svaku metodu i operaciju koja se koristi dano je objašnjenje. Postoji mobilna verzija mrežne stranice, odnosno stranica je prilagođena korištenju na mobilnim uređajima. Sve mogućnosti kalkulatora moguće je koristiti ukoliko postoji Internet veza. Svaka od ovih opcija koje nudi matrični kalkulator vrlo je jednostavan i intuitivan za korištenje kako će se i vidjeti u daljnjem tekstu na primjeru Cramerovog pravila, traženja inverza matrice i množenja matrica.
2.1Cramerovo pravilo
Zbog lakšeg praćenja načina rješavanja tijekom objašnjavanja korištenja Kalkulatora za Cramerovo pravilo rješavat će se sustav tri jednadžbe s tri nepoznanice
\begin{array}{rrr} {2x_{1} -2x_{2} +x_{3} =3} \\ {3x_{1} +x_{2} -x_{3} =7} \\ {x_{1} -3x_{2} +2x_{3} =0} \end{array}
čija su rješenja x_{1} =2,x_{2} =0 i x_{3} =-1.
Klikom na Cramer's Rule u padajućem izborniku na mrežnoj stranici može se izračunati rješenje sustava linearnih jednadžbi pomoću Cramerovog pravila (slika 1).
Slika 1. Izgled Cramer's Rule Calculator
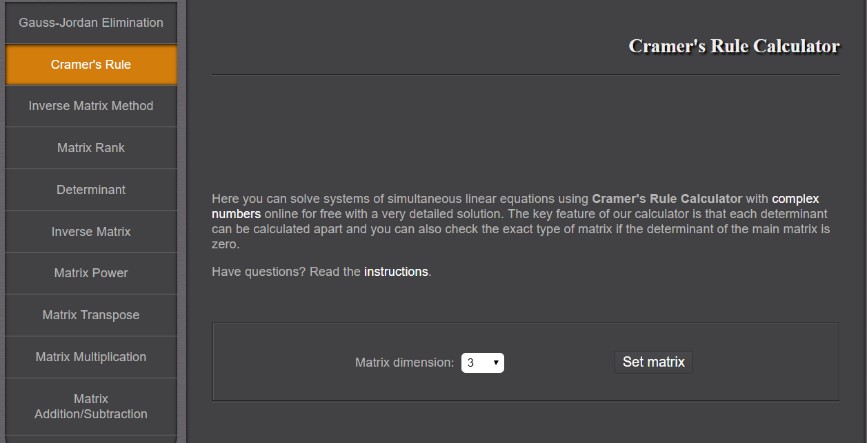 Izvor: autori
Izvor: autori
Otvaranjem Cramer's Rule Calculator prvo treba odabrati red kvadratne matrice (Matrix dimension). Kalkulator izračunava rješenja sustava do 100 jednadžbi s 100 nepoznanica (slika 2).
Slika 2. Odabir dimenzije sustava
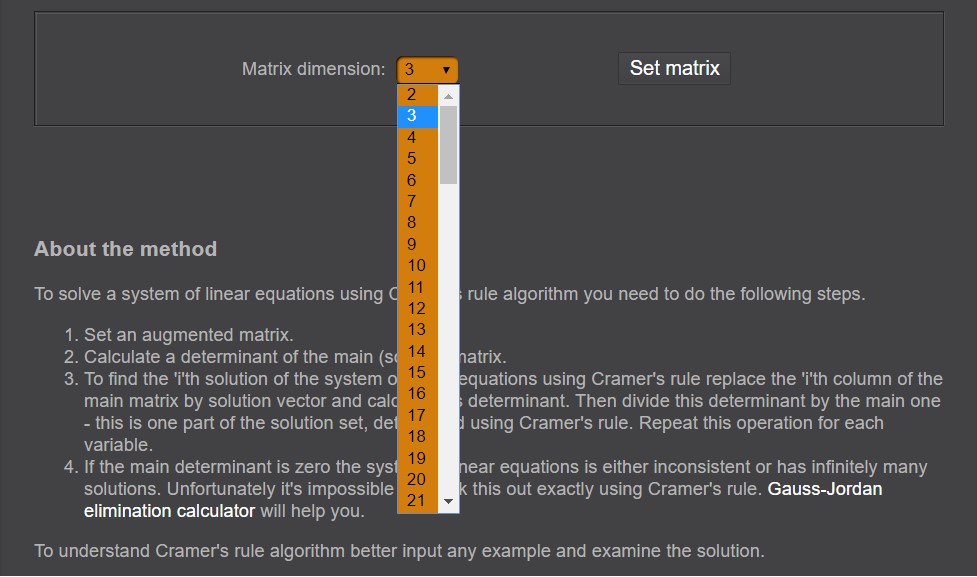 Izvor: autori
Izvor: autori
Klikom na Set matrix pojavljuje se novi prozor u kojem možemo vratiti sustav koji smo prethodno računali klikom na Restore Matrix. Ukoliko rješava sustav koji ima koeficijente kompleksne brojeve potrebno je kliknuti na Complex numbers. U padajućem izborniku Fractional postoji mogućnost odabira zapisa rješenja koje može biti u obliku razlomka ili decimalnog broja. U tablici svaki redak \left(1,2,3\right) predstavlja jednadžbu, a stupac nepoznanice jednadžbi \left(X_{1} ,X_{2} ,X_{3} \right). U ćeliji koja je presjek stupca X_{1} i retka 1 upisuje se koeficijent prve jednadžbe koji se nalazi uz prvu nepoznanicu x_{1}, u ćeliji koja je presjek stupca X_{2} i retka 1 upisuje se koeficijent prve jednadžbe koji se nalazi uz drugu nepoznanicu x_{2}, u ćeliji koja je presjek stupca X_{3}i retka 1 upisuje se koeficijent prve jednadžbe koji se nalazi uz treću nepoznanicu x_{3}i u presjek 1. retka i stupca bupisuje se slobodan član prve jednadžbe. Na isti način se popunjavaju ostali redovi (slika 3).
Slika 3. Upis koeficijenata zadanog sustava jednadžbi
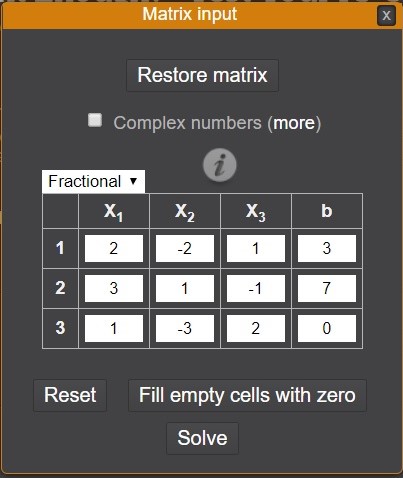 Izvor: autori
Izvor: autori
Reset omogućava brisanje svih podataka koji su unijeti. Fill empty cells with zero omogućava popunjavanje praznih ćelija s nulama, odnosno potrebno je u tablicu unijeti samo koeficijente različite od nule. Klikom na Solve dobiva se rješenje sustava.
Slika 4. Prikaz rješenja sustava
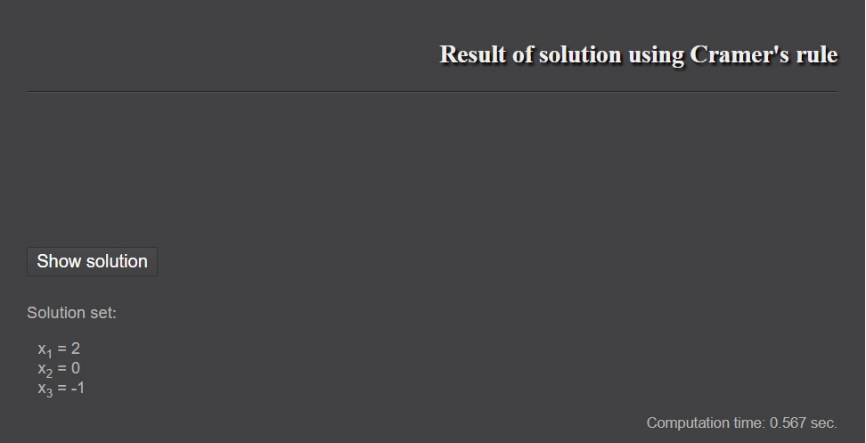 Izvor: autori
Izvor: autori
Rješenje se prikazuje u standardnom obliku za svaku nepoznanicu. U donjem desnom uglu prikazat će se vrijeme potrebno za traženje rješenja zadanog sustava linearnih jednadžbi, a klikom na Show solution prikazat će se korak po korak koji je računat kako bi se došlo do rješenja (slika 4).
Slika 5. Prikaz detaljnog rješenja
 Izvor: autori
Izvor: autori
U detaljnom rješenju prikazane su sve matrice čije se determinante određuju i kvocijent određenih determinanti kako bi se dobilo rješenje (slika 5). Iza svakog zapisa matrice i pripadne determinante postoji opcija Very detailed solution. Klikom na Calculate apart prikazat će se u novom prozoru izračun odabrane determinante.
Slika 6. Prikaz izračuna determinante
 Izvor: Autori
Izvor: Autori
Izračun determinante provodi se svođenjem matrice na gornjotrokutastu matricu pomoću elementarnih transformacija i primjene svojstva da je determinanta trokutaste matrice jednaka umnošku elemenata na glavnoj dijagonali (slika 6).
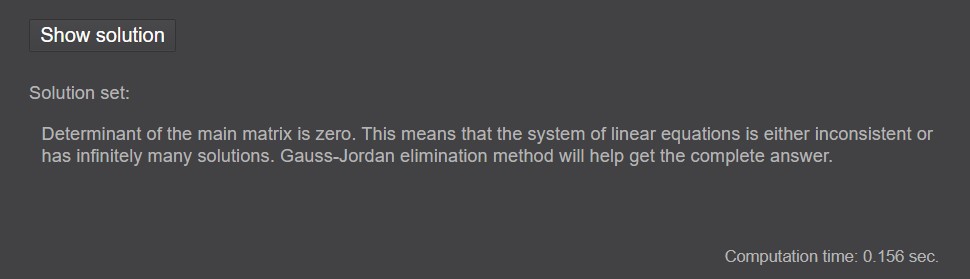
Ukoliko je za uneseni sustav linearnih jednadžbi determinanta glavne matrice, odnosno matrice koja se sastoji od koeficijenata uz nepoznanice sustava linearnih jednadžbi, jednaka nuli, program upućuje na Gauss-Jordanove eliminacije kako bi se dobilo rješenje sustava ukoliko ih ima beskonačno (slika 7).
Slika 7. Rješenje se ne može dobiti primjenom Cramer's Rule Calculator
 Izvor: autori
Izvor: autori
Klikom na Show soulution prikazat će se izračun determinante čija je vrijednost nula.
2.2Inverz matrice
Zbog lakšeg praćenja načina rješavanja tijekom objašnjavanja korištenja Kalkulatora za inverz matrica tražit će se inverz matrice
A=\left[\begin{array}{cc} {1} & {-1} \\ {2} & {3} \end{array}\right].
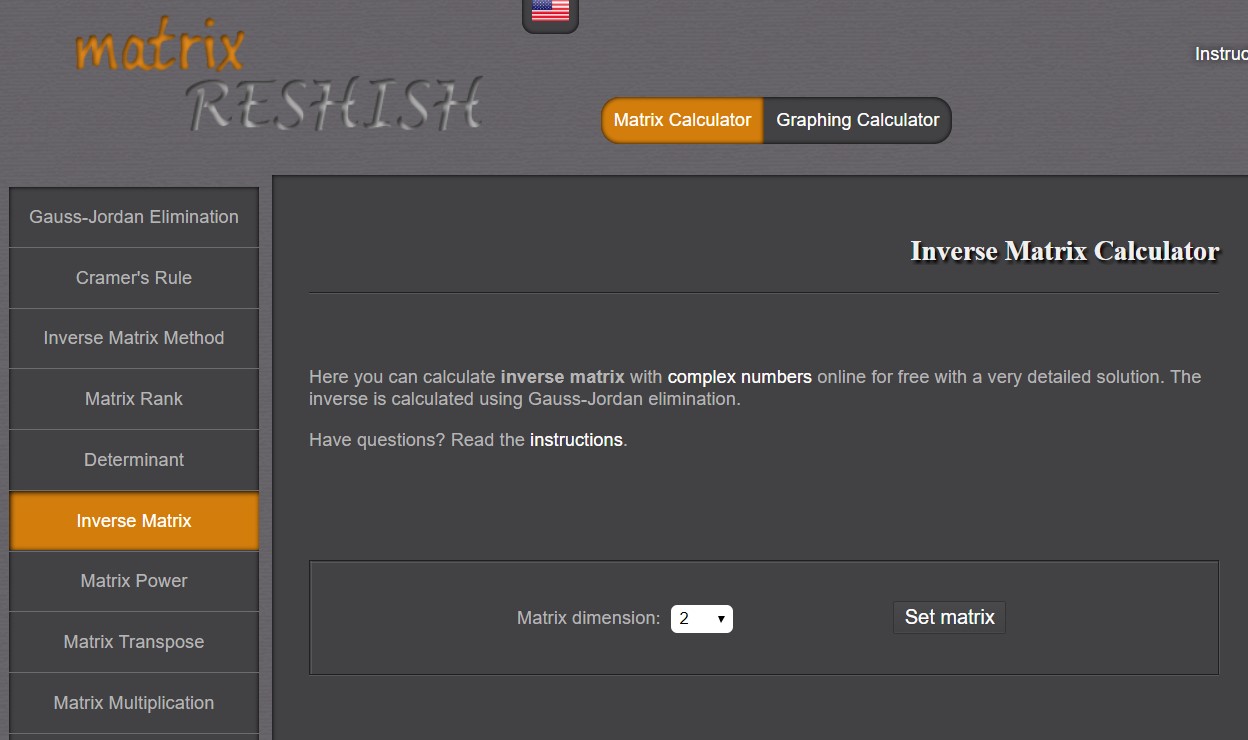
Klikom na Inverse Matrix u padajućem izborniku na mrežnoj stranici možete izračunati inverz matrice (slika 8).
Slika 8. Izgled Inverse Matrix kalkulatora
 Izvor: Autori
Izvor: Autori
Otvaranjem Inverse Matrix Calculator prvo morate odabrati red kvadratne matrice (Matrix dimension). Kalkulator izračunava invez matrice do 100-tog reda. Klikom na Set matrix pojavljuje se novi prozor u kom se upisuju elementi matrice.
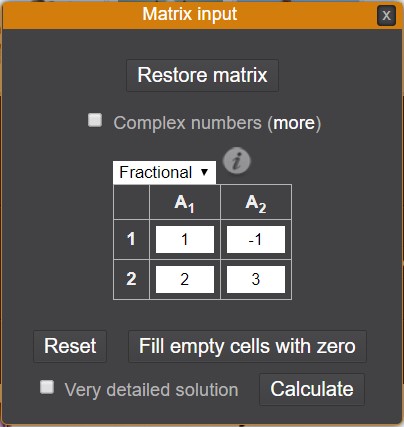
Slika 9. Upis matrice
 Izvor: Autori
Izvor: Autori
Novi prozor za upis elemenata matrice ima sve opcije (Restore matrix, Complex numbers, Reset, Fill empty cells with zero, Calculate) koje su opisane kod Cramer's Rule Calculatora. Novost je opcija Very detailed solution koja ispisuje korak po korak u traženju inverza elementarnim transformacijama (slika 9).
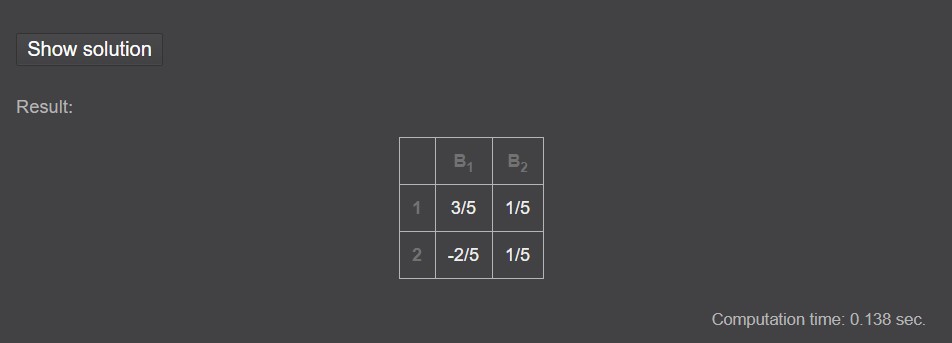
Slika 10. Prikaz rješenja
 Izvor: autori
Izvor: autori
Prikaz rješenja je u matričnom obliku (slika 10). U donjem desnom uglu prikazat će se vrijeme potrebno za izračunavanje inverza, a klikom na Show solution prikazat će se korak po korak koji je računat kako bi se došlo do rješenja (slika 11).
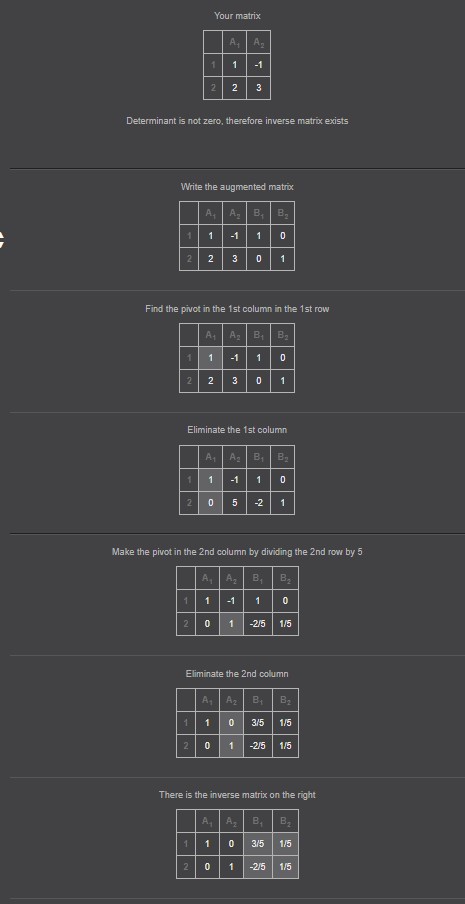
Slika 11. Detaljan prikaz rješenja
 Izvor: autori
Izvor: autori
U detaljnom prikazu rješenja svaka matrica popraćena je s riječima opisanom radnjom u tom koraku. Prvo je izračunata determinanta zadane matrice i provjereno je li ona različita od nule. Odabirom opcije Very detailed solution, odnosno klikom na Calculate apart prikazat će se u novom prozoru. Determinanta se izračunava svođenjem matrice na gornjotrokutastu matricu pomoću elementarnih transformacija i primjene svojstva da je determinanta trokutaste matrice jednaka umnošku elemenata na glavnoj dijagonali.
2.3Množenje matrica
Zbog lakšeg praćenja u primjeru traži se umnožak matrica
A=\left[\begin{array}{cc} {\begin{array}{c} {1} \\ {0} \\ {1} \end{array}} & {\begin{array}{c} {2} \\ {-2} \\ {1} \end{array}} \end{array}\right] i B=\left[\begin{array}{c} {\begin{array}{ccc} {2} & {0} & {-1} \end{array}} \\ {\begin{array}{ccc} {1} & {0} & {4} \end{array}} \end{array}\right].
A\cdot B=\left[\begin{array}{cc} {\begin{array}{c} {1} \\ {0} \\ {1} \end{array}} & {\begin{array}{c} {2} \\ {-2} \\ {1} \end{array}} \end{array}\right]\cdot \left[\begin{array}{c} {\begin{array}{ccc} {2} & {0} & {-1} \end{array}} \\ {\begin{array}{ccc} {1} & {0} & {4} \end{array}} \end{array}\right]=\left[\begin{array}{ccc} {4} & {0} & {7} \\ {-2} & {0} & {-8} \\ {3} & {0} & {3} \end{array}\right].
Klikom na Matrix Multiplication u padajućem izborniku na mrežnoj stranici možete izračunati umnožak matrica (slika 12).
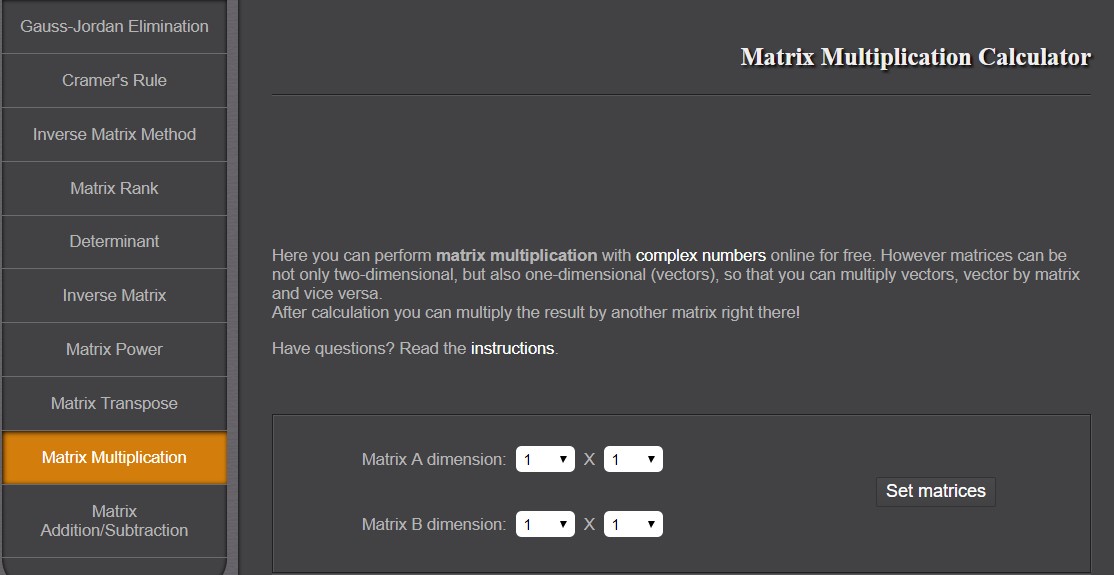
Slika 12. Izgled Matrix Multiplication kalkulatora
 Izvor: autori
Izvor: autori
Otvaranjem Matrix Multiplication Calculator prvo morate odabrati tip matrica (Matrix dimension) koje se množe. Kalkulator izračunava umnožak matrica do tipa 100\times 100. Ukoliko korisnik unese tip matrice koji se ne može množiti, odnosno prva matrica nema onoliko stupaca koliko druga ima redaka, sama aplikacija će automatski promijeniti broj redaka druge matrice ili broj stupaca prve matrice ovisno o tome koju ste dimenziju prvu unijeli. Klikom na Set matrix pojavljuje se novi prozor u kojem se upisuju elementi matrice.
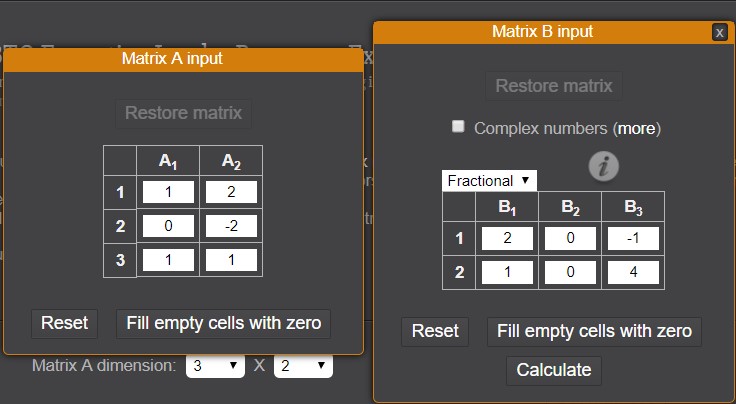
Slika 13. Upis elemenata matrica A i B
 Izvor: autori
Izvor: autori
Elementi matrice A unose se u prvi prozor, a elementi druge matrice u prozor do njega (slika 13). Novi prozor za upis elemenata matrice ima sve opcije (Restore matrix, Complex numbers, Reset, Fill empty cells with zero, Calculate) koje su opisane kod prethodna dva opisana primjera. Klikom na Calculate izračunat će se umnožak matrica.
Slika 14. Prikaz umnoška matrica A i B
 Izvor: autori
Izvor: autori
Prikaz rješenja je u matričnom obliku (slika 14). U donjem desnom uglu prikazat će se vrijeme potrebno za izračunavanje umnoška, a klikom na Show solution prikazat će se korak po korak koji je računat kako bi se došlo do rješenja (slika 15).
Slika 15. Detaljan prikaz rješenja
 Izvor: autori
Izvor: autori
Prikaz detaljnog rješenja se temelji na prikazu matrice u kojem je naznačen element koji se računa, a iznad matrice je zbroj umnožaka koji daje taj element. Element c_{11} nalazi se u prvom retku i prvom stupcu matrice umnoška zadanih matrica. Njegovu vrijednost dobije se zbrajanjem umnožaka prvog retka matrice A i prvog stupca matrice B
c_{11} =1\cdot 2+2\cdot 1=4.
3Prednosti i nedostaci Reshish Matrix kalkulatora
Matrični kalkulator Reshish Matrix besplatan je alat dostupan na računalima i mobilnim uređajima bez dodatnih instalacija. Jedan od nedostataka ovog alata je što se može koristiti samo uz dostupnost internetske veze. Najveća prednost ovog alata je što omogućava 10 različitih operacija s matricama uz detaljan opis svakog koraka računanja rješenja i to matričnog zapisa i opisa riječima.
Tablica 2. Prednosti i nedostaci Reshish Matix alata
|
Prednosti |
Nedostaci |
|
numerički stabilan algoritam, složenosti \mathcal{O}=n^{3} |
ne temelji se na kombinatornom algoritmu |
|
dostupan besplatno |
internetska veza |
|
nije potrebna instalacija |
Laplaceov razvoj |
|
dostupan na mobilnim uređajima |
množenje matrice skalarom |
|
10 različitih operacija |
rješavanje složenijih zadataka s slijedom računskim operacijama |
|
u aritmetici pomičnog zareza Cramerovo pravilo je mnogo točnije |
|
|
detaljan ispis koraka rješenja |
|
|
upis matrica do tipa 100\times 100 |
|
Izvor: autori
Izračun determinante matrice u svakoj ponuđenoj operaciji, u kojoj ju je potrebno računati, računa se pomoću svođenja matrice na trokutastu matricu i računanje pomoću elemenata na glavnoj dijagonali. Nijedna operacija ne pruža mogućnost izračuna determinanti pomoću Laplaceovog razvoja. Laplaceov razvoj je kombinatorni algoritam koji ima složenost \mathcal{O}=n! i numerički je nestabilan. Kombinatorni alati kao Laplaceov razvoj koriste se za simboličku algebru, tj. Computer Algebra Systems (CAS)[6]. Jedan od alata koji daje takvu kombinatornu pomoć je Matrix calculator [7]. Matrix Reshish je numerički alat i ne treba očekivati čisto algebarsko kombinatorni algoritam. Upravo zbog ovoga Cramerovo pravilo je mnogo točnije u aritmetici pomičnog zareza nego isti algoritam temeljen na Laplaceovom razvoju. Za složeniji matrični račun u aritmetici pomičnog zareza može se koristiti Octave Online [8].
Isto tako kalkulator omogućava rješavanje osnovnih računskih operacija, ali ne i traženje rješenja složenijih zadataka s više računskih operacija i primjenom pravila o slijedu računskih operacija, npr. ukoliko su zadane matrice
A=\left[\begin{array}{cc} {\begin{array}{c} {1} \\ {0} \\ {1} \end{array}} & {\begin{array}{c} {2} \\ {-2} \\ {0} \end{array}} \end{array}\right] i B=\left[\begin{array}{c} {\begin{array}{ccc} {2} & {0} & {-1} \end{array}} \\ {\begin{array}{ccc} {1} & {0} & {4} \end{array}} \end{array}\right]
i potrebno je izračunati \left(A\cdot B\right)^{T} +3B-2I u matričnom kalkulatoru posebno se računa umnožak matrica, zatim transponirana matrica umnoška i potom zbroj matrica \left(A\cdot B\right)^{T} +3B, a zatim se dobivenom rezultatu može oduzeti 2I. Množenje matrice skalarom isto tako nije dostupno.
4Zaključak
Reshish Matrix kalkulator je numerički alat koji omogućava izračunavanje osnovnih matričnih operacija i metoda koje se koriste za rješavanje sustava linearnih jednadžbi. Algoritam po kom' radi temelji se na Binet-Caushyevom teoremu i LU rastavu zbog čega je stabilan, a Cramerovo prvilo temeljeno na ovakvom računanju determinante je mnogo točnije u aritmetici pomičnog zareza. Prednosti ovog alata je dostupnost na mobilnim uređajima, te se lako može koristiti u nastavi kao jedan od načina oplemenjivanja nastave. Svaki korak koji je detaljno opisan prilikom rješavanja postavljenog problema uvelike može pomoći studentu prilikom vježbanja i pripremanja ispita.
Bibliografija
|
[1] |
Barnett, R. A., Ziegler, M. R., Byleen, K. E. Primijenjena matematika za poslovanje, ekonomiju, znanost o živom svijetu i humanističke znanosti, Mate d.o.o., Zagreb, 2006. |
|
[2] |
Butković, D., Predavanja iz linearne algebre, Odjel za matematiku, Osijek, 2008. |
|
[3] |
Chiang, A.C. Osnovne metode matematičke ekonomije, treće izdanje, Mate d.o.o., Zagreb, 1994. |
|
[4] |
Divjak, B., Hunjak, T., Matematika za informatičare, TIVA tiskara, Varaždin, 2004. |
|
[5] |
Halusek, V., Špoljarić, M., Matematika za stručni studij ekonomije, Visoka škola za menadžment u turizmu i informatici u Virovitici, Virovitica, 2012. |
|
[6] |
Math Works, https://www.mathworks.com/discovery/computer-algebra-system.html (6.09.2018.) |
|
[7] |
Matrix calculator, http://matrixcalc.org/en/}{http://matrixcalc.org/en/ (6.09.2018.) |
|
[8] |
Octave Online, https://octave-online.net/}{https://octave-online.net/ (6.09.2018.) |
|
[9] |
Reshish Matrix, http://matrix.reshish.com/}{http://matrix.reshish.com/ (4.03.2018.) |
|
[10] |
Scitovski, R., Numerička matematika, Odjel za matematiku, Osijek, 2015.
|